Bài tập mệnh đề lớp 10 chọn lọc, có lời giải - Toán lớp 10

---

Bài tập mệnh đề lớp 10 chọn lọc, có lời giải

Với Bài tập mệnh đề lớp 10 chọn lọc, có lời giải Toán lớp 10 tổng hợp 10 bài tập có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập mệnh đề từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Bài 1: Trong các câu dưới đây, câu nào là mệnh đề, câu nào không phải là mệnh đề. Nếu là mệnh đề thì hãy xét xem nó đúng hay sai:

a) x² + x + 1 > 0

b) 26 chia hết cho 2 và cho 13

c) x² + y² > 9

d) x – 2y và 2 xy

Bài 2:

Các mệnh đề dưới đây thuộc mệnh đề gì và hãy nói nó đúng hay sai:

a) Nếu số a chia hết cho 3 thì a chia hết cho 6.

b) Nếu Δ ABC cân tại A thìΔABC có AB = AC.

c) Tứ giác ABCD là hình vuông khi và chỉ khi ABCD là hình chữ nhật và có AC vuông góc với BD.

Bài 3: Cho tứ giác ABCD, xét hai mệnh đề:

P: " ABCD có tổng hai góc đối bằng 180°"

Q: " ABCD là tứ giác nội tiếp."

Phát biểu mệnh đề P ⇒ Q và cho biết tính đúng, sai của mệnh đề.

Bài 4: Cho ΔABC, xét hai mệnh đề:

P: "ΔABC vuông cân tại A"

Q: "ΔABC là tam giác vuông có AB =AC"

Phát biểu mệnh đề P ⇔ Q bằng hai cách và cho biết mệnh đề này đúng hay sai.

Bài 5: Cho mệnh đề chứa biến P(n): "n(n+1) là số lẻ" với n là số nguyên. Hãy phát biểu các mệnh đề:

a) "∀n ∈ Z ,P(n)" và mệnh đề phủ định của nó.

b) "∃n ∈ Z ,P(n)" và mệnh đề phủ định của nó.

Bài 6: Xét xem các mệnh đề sau đây đúng hay sai và nêu mệnh đề phủ định của mỗi mệnh đề đó:

a)∀n ∈ N^* , n (n² - 1 ) là bội số của 3.

b)∀x ∈ R, x² - 6x + 15 > 0

c) ∃x ∈ R: x² - 6x + 5 = 0

d)∀x ∈ R ,∃y ∈ R:y = x + 3

e)∀x ∈ R ;∀y ∈ R: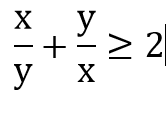

f) ∃n ∈ N ,2ⁿ - 1 là số nguyên tố.

Bài 7: Phát biểu dưới dạng "điều kiện cần" đối với các mệnh đề sau:

a) Hai góc đối đỉnh thì bằng nhau.

b) Hai tam giác có hai cặp cạnh bằng nhau kèm giữa một cặp góc bằng nhau thì bằng nhau.

c) Hai tam giác có hai cặp góc bằng nhau thì bằng nhau.

d) Một số chia hết cho 3 khi và chỉ khi tổng các chữ số chia hết cho 3.

Bài 8: Cho biết tính đúng, sai của các mệnh đề sau. Nếu sai, hãy sửa lại cho đúng:

a) ΔABC đều ⇔ Tam giác có ít nhất một góc bằng 60⁰ .

b) 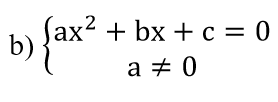có nghiệm kép

⇔Δ=b²-4ac=0.

c) ΔABC cân tại A ⇔ Hai đường cao BE và CF bằng nhau.

d) ∀a,b,c ∈ R:

e) ∀a,b ∈ R: .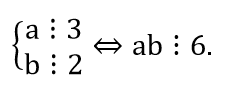

Đáp án và hướng dẫn giải

Bài 1:

a) Đây là mệnh đề và là mệnh đề đúng.

b) Đây là mệnh đề và là mệnh đề đúng.

c) Đây chưa phải là mệnh đề vì chưa khẳng định được tính đúng sai (mệnh đề chưa biến).

d) Đây không phải là mệnh đề.

Bài 2:

a) Đây là mệnh đề kéo theo và là mệnh đề sai. Một số chia hết cho 3 thì không chắc đã chia hết cho 6.

b) Đây là mệnh đề kéo theo và là mệnh đề đúng.

c) Đây là mệnh đề tương đương và là mệnh đề đúng.

Bài 3:

P: "ABCD có tổng hai góc đối bằng 180°"

Q: "ABCD là tứ giác nội tiếp."

P ⇒ Q: Nếu tứ giác ABCD có tổng hai góc đối bằng 180° thì ABCD là tứ giác nội tiếp.

Mệnh đề kéo theo này là mệnh đề đúng.

Bài 4: Cho ΔABC, xét hai mệnh đề:

P: "ΔABC vuông cân tại A"

Q: "ΔABC là tam giác vuông có AB = AC"

P ⇔ Q: ΔABC vuông cân tại A khi và chỉ khi ΔABC là tam giác vuông có

AB = AC.

P ⇔ Q: ΔABC vuông cân tại A là điều kiện cần và đủ để ΔABC là tam giác vuông có AB = AC.

Mệnh đề P ⇔ Q là mệnh đề đúng.

Bài 5: P(n): "n (n + 1) là số lẻ" với n là số nguyên

a) "∀n ∈ Z ,P(n)": Với mọi n thuộc tập số nguyên Z thì n ( n+ 1 ) là số lẻ.

Mệnh đề phủ định: "∃n ∈ Z,P−(n)" : Tồn tại n thuộc tập số nguyên Z sao cho n(n+1) là số chẵn.

b) "∃n ∈ Z ,P(n)": Tồn tại n thuộc tập số nguyên Z để n ( n + 1 ) là số lẻ.

Mệnh đề phủ định: "∀n ∈ Z,P−(n)" : Với mọi n thuộc tập số nguyên Z thì n ( n + 1) là số chẵn.

Bài 6:

a) ∀n ∈ N² , n (n² - 1 ) là bội số của 3: Mệnh đề đúng

Vì: n ( n² -1) = ( n - 1 ) n ( n + 1 ) ⋮3

Mệnh đề phủ định: ∃ n ∈ N² ,n (n² - 1 ) không là bội số của 3.

b) ∀x ∈ R,x² - 6x + 15 > 0: Mệnh đề đúng

Vì x² - 6x + 15 = (x-3) ² + 6 > 0

Mệnh đề phủ định: ∃x ∈ R, x² - 6x + 15 ≤ 0.

c) ∃x ∈ R,x² - 6x +5 = 0 : Mệnh đề đúng

Vì x² - 6x + 5 = 0 ⇔ x = 5 ;x = 1.

Mệnh đề phủ định: ∀ x ∈ R, x² - 6x + 5 ≠ 0

d) ∀x ∈ R,∃y ∈ R: y = x + 3 : Mệnh đề đúng.

Mệnh đề phủ định: ∃x ∈ R ,∀y ∈ R : y ≠ x + 3

e) ∀x ∈ R , ∀y ∈ R: 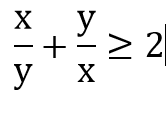:Mệnh đề sai

Vì với x = - 2 ;y = - 2:

Mệnh đề phủ định: ∃x ∈ R , ∃y ∈ R : .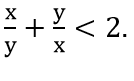

f) ∃n ∈ N,2ⁿ - 1 là số nguyên tố: Mệnh đề đúng

Vì với n = 2: 2² - 1 =3 là số nguyên tố.

Mệnh đề phủ định: ∀n ∈ N ,2ⁿ - 1 không là số nguyên tố.

Bài 7:

a) Hai góc bằng nhau là điều kiện cần để chúng là hai góc đối đỉnh.

b) Hai tam giác bằng nhau là điều kiện cần để chúng có hai cặp cạnh bằng nhau kèm giữa một cặp góc bằng nhau.

c) Hai tam giác có hai cặp góc bằng nhau thì bằng nhau: Đây không phải là mệnh đề đúng nên không viết được với điều kiện cần.

d) Một số chia hết cho 3 là điều kiện cẩn để tổng các chữ số chia hết cho 3.

Bài 8:

a) Δ ABC đều ⇔ Tam giác có ít nhất một góc bằng 60°.

Ta có:

Δ ABC đều ⇒ Tam giác có ít nhất một góc bằng 60° (đúng)

Tam giác có ít nhất một góc bằng 60° ⇒ Δ ABC đều (sai)

Vậy mệnh đề trên sai.

Sửa lại: Δ ABC đều ⇒ Tam giác có ít nhất một góc bằng 60° (đúng)

b) 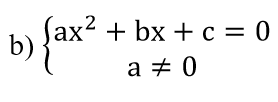có nghiệm kép ⇔Δ = b² - 4ac =0.

Đây là mệnh đề đúng do A ⇒ B đúng và B ⇒ A đúng.

c) Δ ABC cân tại A ⇔ Hai đường cao BE và CF bằng nhau.

Đây là mệnh đề đúng do A ⇒ B đúng và B ⇒ A đúng.

d) ∀a,b,c ∈ R:

Ta có:

∀a,b,c ∈ R: 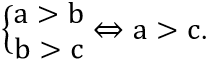: đúng

∀a,b,c ∈ R:a > c ⇒ 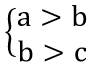: sai

Vậy mệnh đề trên sai.

Sửa lại: ∀a,b,c ∈ R:

e) ∀a,b ∈ R:

Đây là mệnh đề đúng.