Cách giải toán bằng biểu đồ Ven hay, chi tiết - Toán lớp 10

Cách giải toán bằng biểu đồ Ven hay, chi tiết

Với Cách giải toán bằng biểu đồ Ven hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải toán bằng biểu đồ Ven từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Phương pháp giải

- Vẽ các vòng tròn đại diện các tập hợp (mỗi vòng tròn là một tập hợp) lưu ý 2 vòng tròn có phần chung nếu của 2 tập hợp khác rỗng.

- Dùng các biến để chỉ số phần tử của từng phần không giao nhau.

- Từ giả thiết bài toán, lập hệ phương trình và giải tìm các biến.

Ví dụ minh họa

Ví dụ 1:Trong kì thi học sinh giỏi cấp trường, lớp 10A có 17 bạn được công nhận học sinh giỏi văn, 25 bạn học sinh giỏi toán. Tìm số học sinh đạt cả 2 giải văn và toán, biết lớp 10A có 45 bạn và có 13 bạn không đạt học sinh giỏi.

Hướng dẫn:

Biểu diễn tập hợp các học sinh giỏi văn và các học sinh giỏi toán bằng 2 đường cong kín và tập hợp các học sinh lớp 10A bằng hình chữ nhật như hình bên dưới.

Gọi x là số học sinh giỏi văn không giỏi toán; y là số học sinh giỏi cả văn và toán; z là số học sinh chỉ giỏi toán mà không giỏi văn và t là số học sinh không đạt học sinh giỏi.

Theo biểu đồ giả thiết, ta có:

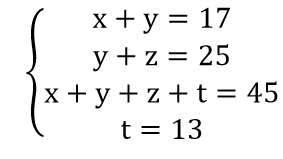
Cộng (1) với (2) rồi trừ cho (3) ta được: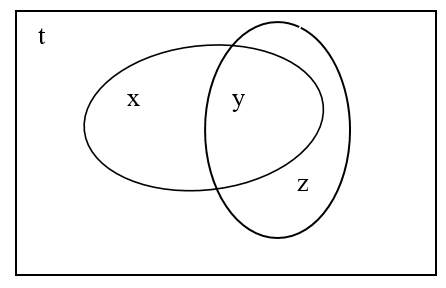

(x + y) + (y + z) – (x + y + z + t) = 17 + 25 - 45

⇒ y - t = - 3 ⇒ y = t – 3 = 10

Vậy lớp 10A có 10 học sinh giỏi cả 2 môn văn và toán.