Các bài toán liên quan đến số gần đúng và sai số và cách giải - Toán lớp 10

---

Các bài toán liên quan đến số gần đúng và sai số và cách giải

Với Các bài toán liên quan đến số gần đúng và sai số và cách giải Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Các bài toán liên quan đến số gần đúng và sai số từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

1. Lý thuyết:

a. Số gần đúng:

Số 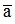biểu thị giá trị thực của một đại lượng gọi là số đúng. Số a có giá trị ít nhiều sai lệch với số đúng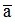gọi là số gần đúng của số.

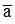b. Sai số tuyệt đối

Nếu a là số gần đúng của số đúng 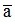thì Δ_a = |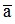- a | gọi là sai số tuyệt đối của số gần đúng a.

c. Độ chính xác của một số gần đúng

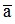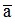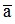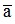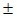Nếu Δ_a = |- a | ≤ d thì a - d ≤ ≤ a + d. Ta nói a là số gần đúng của với độ chính xác d và qui ước viết gọn là = ad

d. Qui tròn số gần đúng

- Nếu chữ số ngay sau hàng qui tròn nhỏ hơn 5 thì ta chỉ việc thay thế chữ số đó và các chữ số bên phải nó bởi số 0.

- Nếu chữ số ngay sau hàng qui tròn lớn hơn hay bằng 5 thì ta thay thế chữ số đó và các chữ số bên phải nó bởi số 0 và cộng thêm một đơn vị vào chữ số ở hàng qui tròn.

2. Phương pháp giải:

- Sai số tuyệt đối của số a là: Δ_a = 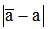với a là số gần đúng của số đúng .

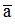- Nếu độ chính xác của phép đo đến hàng phần nghìn thì ta phải quy tròn đến hàng phần trăm; độ chính xác đến hàng phần trăm thì ta phải quy tròn đến hàng phần chục; …

- Nếu độ chính xác của phép đo đến hàng trăm thì ta phải quy tròn đến hàng nghìn; độ chính xác đến hàng nghìn thì ta phải quy tròn đến hàng chục nghìn; …

3. Ví dụ minh họa:

Ví dụ 1:

a. Cho giá trị gần đúng của π là a = 3,141592653589 với độ chính xác là 10^-10 . Hãy viết số quy tròn của a.

b. Cho b = 3,14 và c = 3,1416 là những giá trị gần đúng của π. Hay ước lượng sai số tuyệt đối của b và c.

Hướng dẫn:

a. Vì độ chính xác lên đến hàng phần chục tỉ 10^-10 ( 10 chữ số thập phân sau dấu phẩy) nên ta quy tròn đến hàng phần tỉ 10^-9 ( 9 chữ số thập phân sau dấu phẩy).

Mà sau chữ số 3 ở hàng phần tỉ là chữ số 5 nên theo quy tắc làm tròn số, số quy tròn của a là: 3,141592654.

b. Ta có b = 3,14
Sai số tuyệt đối của b là: Δ = |π - b| < |3,142 – 3,14| = 0,002.

Ta có c = 3,1416

Sai số tuyệt đối của c là: Δ = |π - c| < |3,14159 – 3,1416| = 0,00001.

Ví dụ 2: Hãy viết số quy tròn của số a với độ chính xác d trong các trường hợp sau:

a.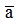= 15,318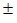0,056.

b.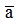= 374529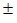200.

Hướng dẫn:

a. Vì độ chính xác đến hàng phần nghìn nên ta quy tròn đến hàng phần trăm. Mà đứng sau số 1 ở hàng phần trăm là số 8 > 5 nên theo quy tắc làm tròn số, số quy tròn của a là: 15,32.

b. Vì độ chính xác đến hàng trăm nên ta quy tròn đến hàng nghìn. Mà đứng sau số 4 ở hàng nghìn là số 5 nên theo quy tắc làm tròn số, số quy tròn của a là: 375000.

Ví dụ 3: Tính đường chéo của một hình vuông có cạnh bằng 3 cm và xác định độ chính xác của kết quả tìm được. Cho biết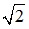 = 1,41412135...

Hướng dẫn:

Ta có đường chéo hình vuông có cạnh bằng 3 cm là: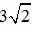cm.

Ta có: 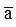= 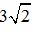; a = 3.1,414 = 4,242 ( với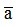là số đúng, a là số gần đúng)

Sai số tuyệt đối là: Δ = |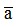- a| = |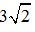- 4,242| < 0,00064

Suy ra độ chính xác là d = 0,00064.

Vậy độ dài đường chéo là 4,242 cm với độ chính xác là 0,00064.

4. Bài tập tự luyện:

Câu 1: Cho giá trị gần đúng của 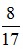là 0,47. Sai số tuyệt đối của số 0,47 là:

A. 0,001.

B. 0,002.

C. 0,003.

D. 0,004.

Hướng dẫn:

Chọn A.

Ta có 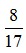= 0,470588235294... nên sai số tuyệt đối của 0,47 là:

Δ = 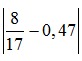< |0,471 - 4,47| = 0,001 .

Câu 2: Cho giá trị gần đúng của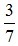là 0,429. Sai số tuyệt đối của số 0,429 là:

A. 0,0001.

B. 0,0002.

C. 0,0004.

D. 0,0005.

Hướng dẫn:

Chọn C.

Ta có 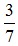= 0,428571... nên sai số tuyệt đối của 0,429 là:

Δ = 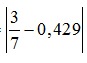< |0,4286 - 0,429| = 0,0004 .

Câu 3: Nếu lấy 3,14 làm giá trị gần đúng của π thì sai số là:

A. 0,001.

B. 0,002.

C. 0,003.

D. 0,004.

Hướng dẫn:

Chọn B.

Ta có π = 3,141592654... nên sai số tuyệt đối của 3,14 là:

Δ = |π - 3,14| < |3,142 - 3,14| = 0,002.

Câu 4: Khi sử dụng máy tính bỏ túi với 10 chữ số thập phân ta được: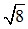= 2,828427125.Giá trị gần đúng của chính xác đến hàng phần trăm là:

A. 2,80.

B. 2,81.

C. 2,82.

D. 2,83.

Hướng dẫn:

Chọn D.

Cần lấy chính xác đến hàng phần trăm nên ta phải lấy 2 chữ số thập phân. Vì đứng sau số 2 ở hàng phần trăm là số 8 > 5 nên theo nguyên lý làm tròn ta được kết quả là 2,83.

Câu 5: Viết giá trị gần đúng của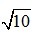chính xác đến hàng phần trăm (dùng máy tính bỏ túi):

A. 3,16.

B. 3,17.

C. 3,10.

D. 3,162.

Hướng dẫn:

Chọn A.

Ta có: 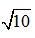= 3,16227766

Cần lấy chính xác đến hàng phần trăm nên ta phải lấy 2 chữ số thập phân. Vì đứng sau số 6 ở hàng phần trăm là số 2 < 5 nên theo nguyên lý làm tròn ta được kết quả là 3,16.

Câu 6: Hãy viết số quy tròn của số a với độ chính xác d được cho sau đây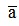= 17658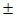16 .

A. 18000.

B. 17800.

C. 17600.

D. 17700.

Hướng dẫn:

Chọn D.

Vì độ chính xác đến hàng chục nên ta quy tròn đến hàng trăm. Mà đứng sau số 6 ở hàng trăm là số 5 nên theo quy tắc làm tròn ta được kết quả là 17700.

Câu 7: Quy tròn số 7216,4 đến hàng đơn vị, được số 7216. Sai số tuyệt đối là:

A. 0,2.

B. 0,3.

C. 0,4.

D. 0,6.

Hướng dẫn:

Chọn C.

Quy tròn số 7216,4 đến hàng đơn vị, được số 7216. Sai số tuyệt đối là:

Δ = |7216,4 - 7216| = 0,4 .

Câu 8: Quy tròn số 2,654 đến hàng phần chục, được số 2,7. Sai số tuyệt đối là:.

A. 0,05.

B. 0,04.

C. 0,046.

D. 0,1.

Hướng dẫn:

Chọn C.

Quy tròn số 2,654 đến hàng phần chục, được số 2,7. Sai số tuyệt đối là: |2,654 - 2,7| = 0,046.

Câu 9: Một hình chữ nhật có các cạnh: x = 4,2m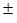1cm, y = 7m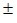2cm. Chu vi của hình chữ nhật và độ chính xác của giá trị đó.

A. 22,4 m và 3 cm.

B. 22,4 m và 1 cm.

C. 22,4 m và 2 cm.

D. 22,4 m và 6 cm.

Hướng dẫn:

Chọn D.

Chu vi hình chữ nhật là: P = 2.(x + y) = 2.[(4,2 + 7)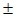(1 + 2)] = 22,4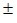cm6cm .

Vậy chu vi hình chữ nhật là 22,4 m và độ chính xác là 6 cm.

Câu 10: Cho tam giác ABC có độ dài ba cạnh đo được như sau a = 12cm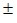 0,2cm; b = 10,2cm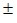0,2cm; c = 8cm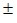0,1cm . Tính chu vi P của tam giác đã cho.

A. 30,2cm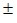0,2cm .

B. 30,2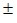cm1cm .

C. 30,2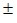cm0,5cm

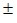D. 30,2cm2cm .

Hướng dẫn:

Chọn C.

Chu vi tam giác ABC là:

P = a + b+ c = (12 + 10,2 + 8)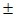 (0,2 + 0,2 + 0,1) = 30,2 cm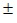0,5 cm.