Các dạng bài tập về toạ độ của vectơ, toạ độ của một điểm và cách giải - Toán lớp 10

---

Các dạng bài tập về toạ độ của vectơ, toạ độ của một điểm và cách giải

Với Các dạng bài tập về toạ độ của vectơ, toạ độ của một điểm và cách giải Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập toạ độ của vectơ, toạ độ của một điểm từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Lí thuyết.

- Tọa độ của điểm trên trục: Cho M là một điểm tùy ý trên trục (O;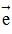). Khi đó tồn tại duy nhất một số k sao cho 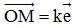. Ta gọi số k đó là tọa độ của điểm M trên trục (O; ).

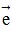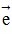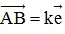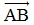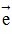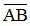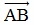- Tọa độ của vectơ trên trục: Cho hai điểm A và B trên trục (O; ). Khi đó tồn tại duy nhất một số k sao cho . Độ dài đại số của đối với trục (O; ) kí hiệu là . Nếu cùng hướng vớ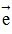i thì 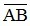> 0 . Nếu 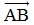ngược hướng vớ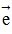i thì 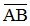< 0 . Nếu hai điểm A và B trên trục (O; 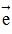) có tọa độ lần lượt là a và b thì 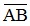= b – a.

- Tọa độ trung điểm I đoạn thẳng AB trên trục (O;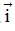) là: x_I = .

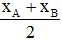- Tọa độ của vectơ trong mặt phẳng Oxy: Có 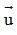= (x;y) ⇔ 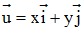. Cho hai điểm A(x_A;y_A) và B(x_B;y_B) ta có: 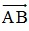= ( x_B - x_A; y_B - y_A).

- Tọa độ của điểm trong mặt phẳng Oxy: Có M(x;y) ⇔ .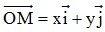

- Tọa độ trung điểm I(x_I;y_I) của đoạn thẳng AB là:x_I = 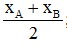; y_I = .

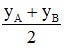- Tọa độ của trọng tâm G(x_G;y_G) của tam giác ABC được tính theo công thức: x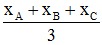_G = ;y_G =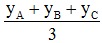

- Điều kiện để hai vectơ cùng phương: Hai vectơ 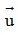= (u₁;u₂) và 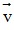= (v₁;v₂) với 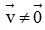cùng phương khi và chỉ khi có số k sao cho u₁ = kv₁ và u₂ = kv₂ . Nếu k > 0 thì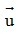cùng hướng với 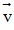, ngược lại, nếu k < 0 thì 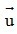ngược hướng với .

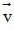- Hai vectơ bằng nhau khi chúng có hoành độ bằng nhau và tung độ bằng nhau.

- Cho 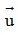= (u₁;u₂) và 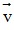= (v₁;v₂) , khi đó:

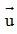+= (u₁ + v₁; u₂ + v₂)

-= (u₁ - v₁; u_{2 -} v₂)

k. = (ku₁;ku₂) , k ∈ R .

B. Các dạng bài.

Dạng 1: Tìm tọa độ của một điểm, tọa độ của vectơ trên trục (O; 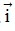) và trong mặt phẳng Oxy.

Phương pháp giải:

Áp dụng lí thuyết về tọa độ của điểm, tọa độ của vectơ trên trục và tọa độ của điểm, tọa độ của vectơ trong mặt phẳng Oxy, tọa độ của trung điểm đoạn thẳng, tọa độ của trọng tâm tam giác, các tính chất của vectơ để xác định tọa độ của điểm và tọa độ của vectơ theo yêu cầu đề bài.

Ví dụ minh họa:

Bài 1: Trên trục tọa độ (O;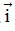) cho 2 điểm A, B có tọa độ lần lượt là -2; 1. Tìm tọa độ của vectơ 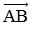và tọa độ trung điểm I của đoạn thẳng AB.

Giải:

Ta có: 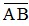= x_B - x_A = 1 - (-2) = 1 + 2 = 3

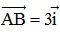⇒ ⇒ Tọa độ của vectơ 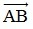trên trục tọa độ (O;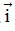) là 3.

Tọa độ điểm I là: x_I = .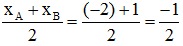

Bài 2: Trong mặt phẳng Oxy, cho 3 điểm A (-3;1), B (2;4) và C (2;1). Tìm tọa độ trọng tâm G của tam giác ABC, tọa độ trung điểm đoạn thẳng AB, AC.

Giải:

Áp dụng công thức tọa độ trọng tâm tam giác ta có:

x_G =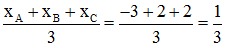

y_G = 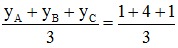= 2

⇒ G =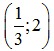

Áp dụng công thức tọa độ trung điểm đoạn thẳng ta có:

Gọi I là trung điểm của đoạn thẳng AB có:

x_I =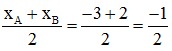

y_I =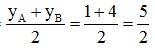

⇒ I =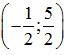

Gọi J là trung điểm của đoạn thẳng AC có:

x_J =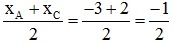

y_J = 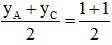= 1

⇒ J =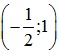

Dạng 2: Xác định tọa độ điểm, vectơ liên quan đến biểu thức dạng 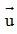+ 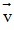, 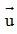- 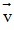và k .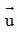

Phương pháp giải:

Áp dụng công thức tính tọa độ của các vectơ 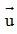+ 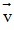, 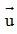- 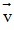và k .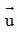

Ví dụ minh họa:

Bài 1: Cho hai vectơ 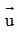= (3;-2) và 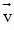= (1;6) . Tính tọa độ các vectơ 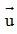+ 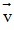, 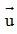- 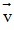và k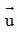 với k = 5.

Giải:

+) Ta có: 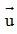+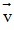= (u₁ + v₁; u₂ + v₂) = ( 3 + 1 ; -2 + 6 ) = (4;4).

+) Ta có: 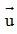-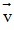= (u₁ - v₁; u₂ - v₂) = ( 3 - 1 ; -2 - 6 ) = (2;-8)

+) Ta có: k.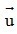 = (ku₁;ku₂) = (5.3;-2.5) = (15; -10)

Bài 2: Trong mặt phẳng Oxy, cho các điểm A (1;3) và B (4;0). Tìm tọa độ điểm M thỏa mãn .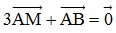

Giải:

Gọi tọa độ điểm M là ( x;y)

+) Tọa độ vectơ 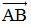là: 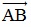= ( 4 – 1 ; 0 – 3 ) = ( 3;-3 )

+) Tọa độ vectơ 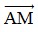là: 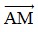= ( x – 1 ; y – 3 )

+) Ta có: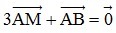

⇒

⇔

⇔

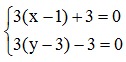
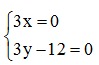
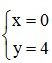
M = ( 0;4 )

Dạng 3: Bài toán liên quan đến sự cùng phương của hai vectơ. Phân tích một vectơ qua hai vectơ không cùng phương.

Phương pháp giải:

Áp dụng điều kiện để hai vectơ cùng phương liên quan đến tọa độ: Hai vectơ 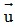(u₁;u₂) và 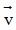= (v₁;v₂) với 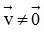cùng phương khi và chỉ khi có một số k sao cho u₁ = kv₁ và u₂ = kv₂ . Nếu k > 0 thì 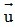cùng hướng với 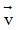, ngược lại, nếu k < 0 thì 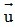ngược hướng với 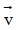. Để phân tích 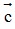(c₁;c₂) qua hai vectơ 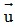(u₁;u₂) và 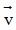= (v₁;v₂) không cùng phương, ta giả sử 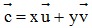. Khi đó ta quy về giải hệ phương trình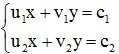

Ví dụ minh họa:

Bài 1: Cho A (1;2), B (-2;6). Điểm M nằm trên trục Oy sao cho ba điểm A, B, M thẳng hàng. Tìm tọa độ điểm M .

Giải:

Ta có: M nằm trên trục Oy ⇒ M = (0;y)

Ta có: 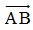= (-3;4), 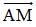= (1; y - 2) .

Ba điểm A, B, M thẳng hàng ⇒ 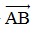cùng phương với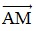

⇒

⇔

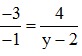
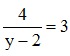
⇔ 3y – 6 = 4

⇔ y =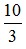

⇒ M =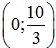

Bài 2: Cho các vectơ 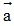= (4;-2), 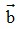= (-1;-1) và 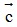=(2;5) . Phân tích vectơ 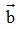theo hai vectơ 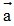và .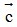

Giải:

Giả sử ⇒ ⇒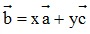

⇒

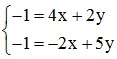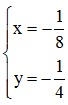
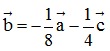
C. Bài tập tự luyện.

Bài 1: Trên trục tọa độ (O; 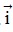) cho 2 điểm A, B có tọa độ lần lượt là 3 và -5. Tìm tọa độ trung điểm I của đoạn thẳng AB.

Đáp án: x_I = -1.

Bài 2: Trong mặt phẳng Oxy, cho điểm M (x;y). Tìm tọa độ của điểm M’ đối xứng với M qua trục hoành.

Đáp án: M’ (x;-y)

Bài 3: Trong mặt phẳng Oxy, cho hình vuông ABCD tâm I và có A (1;3). Biết điểm B thuộc trục Ox và 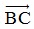cùng hướng với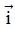. Tìm tọa độ vectơ .

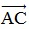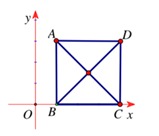
Đáp án: 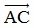= (3;-3)

Bài 4: Trong mặt phẳng Oxy, cho hình thoi ABCD cạnh a. Biết ∠BAD = 60^o, A trùng với gốc tọa độ O; C thuộc Ox và x_B ≥ 0, y_B ≥ 0. Tìm tọa độ đỉnh B, C của hình thoi ABCD.

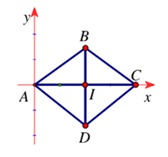
Đáp án: B = 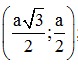; C = (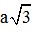; 0)

Bài 5: Cho 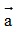= (x;2) ,(-5;1) và 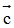= (x;7) . Vectơ 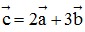. Tìm x.

Đáp án: x = 15.

Bài 6: Trong mặt phẳng Oxy, cho các điểm A (-3;3) , B (1;4) , C (2;-5). Tìm tọa độ điểm M thỏa mãn: .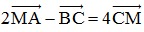

Đáp án: M =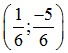

Bài 7: Cho 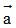= (0;1), 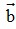= ( -3;-2),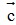= (-1;2) . Tính tọa độ vectơ .

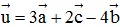Đáp án: 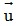= (10;15)

Bài 8: Cho 4 điểm A (1;-2) , B (0;3) , C (-3;4) , D (-1;8). Ba điểm nào trong 4 điểm đã cho là thẳng hàng ?

Đáp án: Ba điểm A, B, D.

Bài 9: Trong mặt phẳng Oxy, cho ba điểm A (6;3) , B (-3;6) . Xác định điểm D trên trục tung sao cho A, B, D thẳng hàng.

Đáp án: D = (0;5)

Bài 10: Trong mặt phẳng Oxy, cho A (m-1;-1) , B (2;2-2m) , C (m+3;3). Tìm m để A, B, C là ba điểm thẳng hàng.

Đáp án: m = 0.