Tính tích của vectơ với một số và cách giải - Toán lớp 10
Tính tích của vectơ với một số và cách giải
Với Tính tích của vectơ với một số và cách giải Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tích của vectơ với một số từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

A. Lí thuyết.
- Tích của vectơ với một số: Cho số k ≠ 0 và vectơ 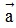 ≠
≠ 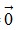 . Tích của vectơ
. Tích của vectơ 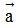 với số k là một vectơ, kí hiệu là k
với số k là một vectơ, kí hiệu là k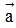 , cùng hướng với
, cùng hướng với 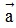 nếu k > 0, ngược lại, ngược hướng với
nếu k > 0, ngược lại, ngược hướng với 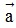 nếu k < 0 và có độ dài bằng |k||
nếu k < 0 và có độ dài bằng |k||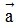 | .
| .
- Tính chất: Với hai vectơ 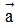 và
và 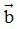 bất kì, với mọi số h và k, ta có:
bất kì, với mọi số h và k, ta có:
+) k(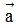 +
+ 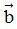 ) = k
) = k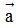 + k
+ k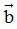
+) (h + k)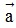 = h
= h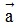 + k
+ k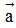
+) h (k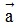 ) = (hk)
) = (hk)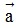
+) 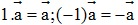
- Quy tắc trung điểm: Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có: 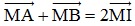
- Quy tắc trọng tâm: Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M ta có: 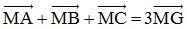
- Điều kiện để hai vectơ cùng phương: Cho hai vectơ 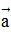 và
và 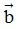 (
( 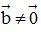 ) ,
) ,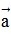 và
và 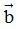 cùng phương khi và chỉ khi tồn tại số k để
cùng phương khi và chỉ khi tồn tại số k để 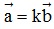 .
.
- Điều kiện ba điểm thẳng hàng: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có tồn tại một số k khác 0 để 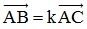 .
.
- Chú ý: Đối với vectơ – không : 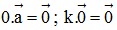 .
.
B. Các dạng bài.
Dạng 1: Tính độ dài vectơ khi biết tích vectơ với một số.
Phương pháp giải:
Sử dụng định nghĩa tích của vectơ với một số, các quy tắc về tổng, hiệu của các vectơ và các hệ thức lượng, định lý Py-ta-go để tính độ dài vectơ đó.

Ví dụ minh họa:
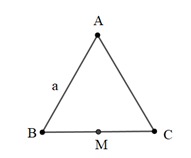
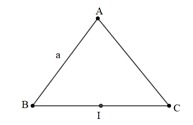
Bài 1: Cho tam giác ABC đều cạnh a. Biết M là trung điểm BC. Tính độ dài vectơ 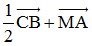 .
.
Giải:
Ta có: CM = 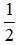 CB (do M là trung điểm BC) và B, C, M thẳng hàng.
CB (do M là trung điểm BC) và B, C, M thẳng hàng.
⇒ 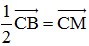
⇒ 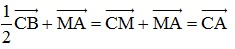
⇒ 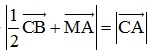 = CA = a (ABC là tam giác đều cạnh a)
= CA = a (ABC là tam giác đều cạnh a)
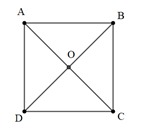
Bài 2: Cho hình vuông ABCD cạnh 2a tâm O. Tính độ dài vectơ 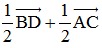 .
.
Giải:
+) Vì B, O, D thẳng hàng và OD = 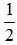 BD (do O là tâm hình vuông ABCD)
BD (do O là tâm hình vuông ABCD)
⇒ 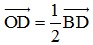
+) Vì A, O, C thẳng thàng và OC = 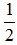 AC (do O là tâm hình vuông ABCD)
AC (do O là tâm hình vuông ABCD)
⇒ 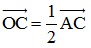
+) Ta có: 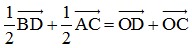
+) Áp dụng quy tắc hình bình hành ta có: 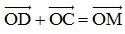 .
.
+) Xét hình bình hành OCMD có:
∠COD = 90o
OC = OD
⇒ OCMD là hình vuông.
+) Xét tam giác DAB vuông tại A
Áp dụng định lý Py-ta-go ta có:
BD2 = AD2 + AB2
⇒ BD2 = (2a)2 + (2a)2 =8a2
⇒ BD = 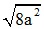 =2
=2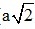
⇒ OD = OC =  BD =
BD =  .2
.2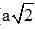 =
= 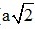
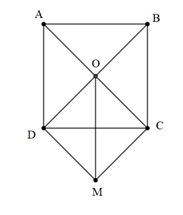
+) Xét tam giác ODM vuông tại D
DM = OC = 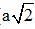 ( do OCMD là hình vuông)
( do OCMD là hình vuông)
Áp dụng định lý Py-ta-go ta có:
OM2 = OD2 + DM2
⇒ OM2 = (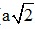 )2 + (
)2 + ( 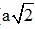 )2 = 4a2
)2 = 4a2
⇒ OM = 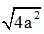 = 2a
= 2a
⇒ 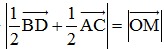 = OM = 2a
= OM = 2a
Dạng 2: Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước.
Phương pháp giải:
Biến đổi đẳng thức đã cho về dạng 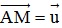 trong đó A là một điểm cố định,
trong đó A là một điểm cố định, 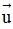 cố định và dựng điểm M là điểm thỏa mãn
cố định và dựng điểm M là điểm thỏa mãn 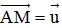 .
.

Ví dụ minh họa:
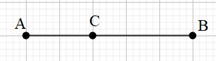
Bài 1: Cho hai điểm phân biệt A và B. Tìm điểm C sao cho 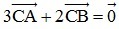 .
.
Giải:
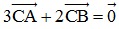
⇒ 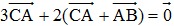
⇒ 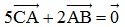
⇒ 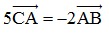
⇒ 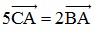
⇒ 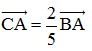
Vậy ta dựng được điểm C thỏa mãn C, A, B thẳng hàng và CA = 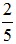 AB .
AB .
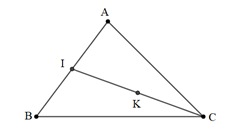
Bài 2: Cho tam giác ABC. Tìm điểm K sao cho: 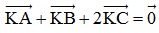
Giải:
+) Ta có: 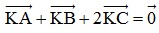
⇔ 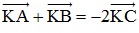
⇔ 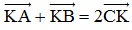 (1)
(1)
+) Gọi I là trung điểm của AB. ⇒ 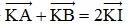 (2)
(2)
+) Từ (1) và (2) ⇒ 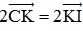 ⇔
⇔ 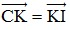
Vậy ta dựng được điểm K là trung điểm của CI.

C. Bài tập tự luyện.
Bài 1: Cho tam giác đều ABC cạnh a, I là trung điểm BC. Tính độ dài vectơ 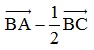
Đáp án: 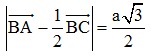
Bài 2: Cho hình vuông ABCD tâm O cạnh a. Biết K là trung điểm của OD. Tính độ dài vectơ 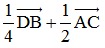 .
.
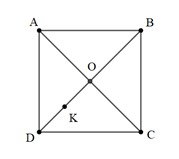
Đáp án: 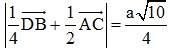
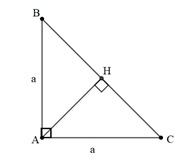
Bài 3: Cho tam giác vuông ABC có đường cao AH. Biết AB = AC = a. Tính độ dài vectơ 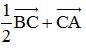 .
.
Đáp án: 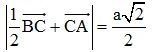
Bài 4: Cho hình vuông ABCD cạnh a tâm O. Cho M là điểm có vị trí tùy ý. Tính độ dài vectơ 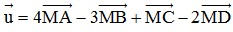 .
.
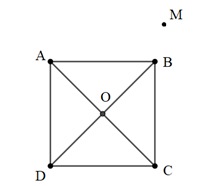
Đáp án: 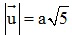
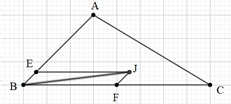
Bài 5: Cho tam giác ABC, có điểm E trên AB sao cho EB =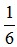 AB và điểm F là trung điểm của BC. Biết
AB và điểm F là trung điểm của BC. Biết 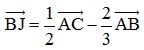 . Dựng điểm J.
. Dựng điểm J.
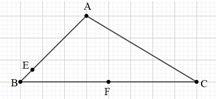
Đáp án:
Bài 6: Cho tam giác ABC. Dựng điểm O sao cho 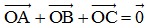 .
.
Đáp án: O là trọng tâm tam giác ABC.
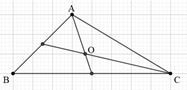
Bài 7: Cho tứ giác ABCD. Biết M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Dựng điểm I sao cho 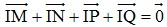 .
.
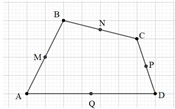
Đáp án:
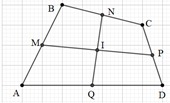
Bài 8: Cho tam giác ABC. Tìm điểm J sao cho 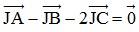 . Biết I là trung điểm của AB.
. Biết I là trung điểm của AB.
Đáp án:
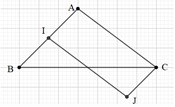
Bài 9: Cho 4 điểm A, B, C, M. Tìm điểm C sao cho 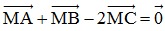 .
.
Đáp án: C là trung điểm của AB.
Bài 10: Cho 3 điểm M, P, Q. Tìm điểm M sao cho 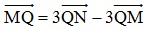 .
.
Đáp án: