Sử dụng sơ đồ hình cây lớp 10 (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Sử dụng sơ đồ hình cây lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Sử dụng sơ đồ hình cây.

Sử dụng sơ đồ hình cây lớp 10 (bài tập + lời giải)

1. Phương pháp giải

Phương pháp tính xác suất của biến cố E theo định nghĩa cổ điển:

− Bước 1. Tính số phần tử của không gian mẫu là n(Ω).

− Bước 2. Tính số phần tử của biến cố E là n(E).

− Bước 3. Tính xác suất theo công thức: $P\left(E\right)=\frac{n\left(E\right)}{n\left(\Omega \right)}.$

Để tính số phần tử của không gian mẫu và biến cố E trong Bước 1, Bước 2, ta có thể sử dụng sơ đồ hình cây mô tả một cách trực quan những kết quả xảy ra/ kết quả thuận lợi.

*Chú ý: Ta sử dụng sơ đồ hình cây trong một số bài toán, phép thử T được hình thành từ một vài phép thử, chẳng hạn: giao xúc xắc liên tiếp 4 lần; lấy 3 viên bi, mỗi viên từ một hộp; …

2. Ví dụ minh họa:

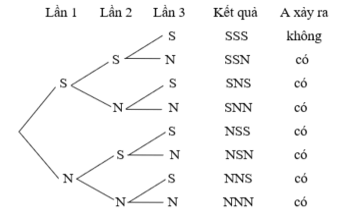
Ví dụ 1. Tung một đồng xu cân đối và đồng chất 3 lần liên tiếp. Tính xác suất của biến cố A: “Trong 3 lần tung có ít nhất 1 lần xuất hiện mặt ngửa”.

Hướng dẫn giải:

Kí hiệu S nếu tung đồng xu được mặt sấp, N nếu tung đồng xu được mặt ngửa.

Các kết quả có thể xảy ra trong 3 lần tung được thể hiện trong sơ đồ hình cây dưới đây:

Có tất cả 8 kết quả xảy ra, trong đó có 7 kết quả thuận lợi cho biến cố A.

Do đó: $\text{P}\left(A\right)\text{ = }\frac{\text{7}}{\text{8}}$

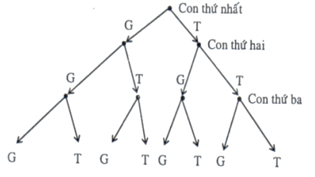
Ví dụ 2. Chọn ngẫu nhiên một gia đình có ba con và quan sát giới tính của ba người con này. Tính xác suất của các biến cố sau:

a) A: "Con đầu là gái";

b) B: "Có ít nhất một người con trai".

Hướng dẫn giải:

Các trường hợp có thể xảy đối với một gia đình 3 con có thể mô tả bằng sơ đồ dưới đây:

Theo sơ đồ trên ta thấy có 8 trường hợp có thể xảy ra.

a) A: "Con đầu là gái"

Quan sát sơ đồ, ta thấy các kết quả thuận lợi cho biến cố A là: {GGG; GGT; GTG; GTT}.

Do đó, có 4 kết quả thuận lợi cho biến cố A.

Vậy xác suất của biến cố B là: $\text{P}\left(\text{A}\right)\text{ = }\frac{4}{\text{8}}=\frac{1}{2}$.

b) B: "Có ít nhất một người con trai"

 Quan sát sơ đồ, ta thấy các kết quả thuận lợi cho biến cố B là: {GGT; GTG; GTT; TGG; TGT; TTG; TTT}.

Do đó, có 7 kết quả thuận lợi cho biến cố B.

Vậy xác suất của biến cố B là: $\text{P}\left(B\right)=\frac{7}{8}.$

3. Bài tập tự luyện 

Bài 1. Có ba chiếc hộp. Hộp I có chứa ba viên bi: 1 viên màu đỏ, 1 viên màu xanh và 1 viên màu vàng. Hộp II chứa hai viên bi: 1 viên màu xanh và 1 viên màu vàng. Hộp III chứa hai viên bi: 1 viên màu đỏ và 1 viên màu xanh. Từ mỗi hộp ta lấy ngẫu nhiên một viên bi. Xác suất để trong ba viên bi lấy ra có đúng một viên bi màu xanh là

A. $\frac{5}{12}$;

B. $\frac{5}{6}$;

C. $\frac{1}{6}$;

D. $\frac{1}{12}$.

Bài 2. Chọn ngẫu nhiên một gia đình có ba con và quan sát giới tính của ba người con này. Xác suất để có đúng 2 con gái là

A. $\frac{1}{4}$;

B. $\frac{1}{2}$;

C. $\frac{7}{8}$;

D. $\frac{3}{8}$.

Bài 3. Chọn ngẫu nhiên một gia đình có ba con và quan sát giới tính của ba người con này. Xác suất để không có con trai là

A. $\frac{1}{4}$;

B. $\frac{1}{8}$;

C. $\frac{7}{8}$;

D. $\frac{3}{8}$.

Bài 4. Tung một đồng xu cân đối và đồng chất 3 lần liên tiếp. Xác suất của biến cố A: “Trong 3 lần tung có 2 lần xuất hiện mặt ngửa” là

A. $\frac{1}{4}$;

B. $\frac{1}{8}$;

C. $\frac{1}{6}$;

D. $\frac{3}{8}$.

Bài 5. Gieo liên tiếp một đồng xu cân đối và một con xúc xắc cân đối. Xác suất đồng xu xuất hiện mặt ngửa là

A. $\frac{1}{4}$;

B. $\frac{1}{2}$;

C. $\frac{1}{6}$;

D. $\frac{5}{12}$.

Bài 6. Gieo liên tiếp một đồng xu cân đối và một con xúc xắc cân đối. Xác suất đồng xu xuất hiện mặt sấp hoặc số chấm xuất hiện trên con xúc xắc là 5 là

A. $\frac{1}{2}$;

B. $\frac{1}{6}$;

C. $\frac{5}{12}$;

D. $\frac{7}{12}$.

Bài 7. Gieo một đồng xu cân đối liên tiếp bốn lần. Xác suất để trong bốn lần gieo đó có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa là

A. $\frac{1}{4}$;

B. $\frac{1}{8}$;

C. $\frac{5}{16}$;

D. $\frac{3}{8}$.

Bài 8. Gieo một đồng xu cân đối liên tiếp bốn lần. Xác suất để trong bốn lần gieo đó có ít nhất 2 lần xuất hiện mặt sấp là

A. $\frac{11}{16}$;

B. $\frac{5}{16}$;

C. $\frac{5}{8}$;

D. $\frac{3}{8}$.

Bài 9. Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh, 1 thẻ đỏ. Các tấm thẻ có kích thước có khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ. Xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 1 thẻ màu đỏ” là

A. $\frac{1}{3}$;

B. $\frac{2}{3}$;

C. $\frac{1}{6}$;

D. $\frac{1}{2}$.

 Bài 10. Dự báo thời tiết trong ba ngày thứ Hai, thứ Ba, thứ Tư của tuần sau cho biết, trong mỗi ngày này, khả năng có mưa và không mưa như nhau. Xác suất biến cố trong 3 ngày, có đúng 1 ngày mưa là

A. $\frac{1}{8}$;

B. $\frac{1}{2}$;

C. $\frac{3}{8}$;

D. $\frac{7}{8}$.