Ứng dụng để giải các bài toán thực tế (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Ứng dụng để giải các bài toán thực tế lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Ứng dụng để giải các bài toán thực tế.

Ứng dụng để giải các bài toán thực tế (bài tập + lời giải)

1. Phương pháp giải

Bài toán: Ứng dụng phương trình quy về phương trình bậc hai để giải các bài toán thực tế.

Để giải bài toán trên, ta thực hiện các bước sau:

Bước 1. Đặt ẩn cho đại lượng cần tìm và biểu diễn các đại lượng liên quan.

Bước 2. Lập phương trình biểu diễn các giả thiết.

Bước 3. Giải phương trình và kết luận.

2. Ví dụ minh họa:

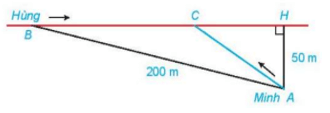
Ví dụ. Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa điểm B, cách mình một đoạn 200 m thì Minh bắt đầu đi bộ ra lề đường để bắt kịp xe. Vận tốc đi bộ của Minh là 5 km/h, vận tốc xe đạp của Hùng là 15 km/h. Hãy xác định vị trí C trên lề đường (hình vẽ) để hai bạn gặp nhau mà không bạn nào phải chờ người kia (làm tròn kết quả đến hàng phần mười)

Hướng dẫn giải:

Vận tốc của bạn Minh: v₁ = 5 km/h.

Vận tốc của bạn Hùng: v₂ = 15 km/h.

Áp dụng định lý Pythagore vào tam giác AHB vuông tại H ta có:

$BH=\sqrt{A{B}^2-A{H}^2}=\sqrt{{\left(0,2\right)}^2–{\left(0,05\right)}^2}=\frac{\sqrt{15}}{20}$ (km)

Gọi BC = x (km), x > 0.

Suy ra: $CH=BH–BC=\frac{\sqrt{15}}{20}–x, x\le \frac{\sqrt{15}}{20}$

Ta cần xác định vị trí điểm C để Minh và Hùng gặp nhau mà không bạn nào phải chờ người kia.

Nghĩa là: ta cần tìm x để thời gian hai bạn di chuyển đến C là bằng nhau.

Thời gian Hùng đi từ B đến C là: $t_2=\frac{S_{BC}}{v_2}=\frac{x}{15}$ (h).

Đổi 50 m = 0,05 km. Quãng đường AC mà Minh đã đi là:

$AC=\sqrt{C{H}^2+A{H}^2}=\sqrt{{\left(\frac{\sqrt{15}}{20}–x\right)}^2+{\left(0,05\right)}^2}$

$t_1=\frac{S_{AC}}{v_1}=\frac{\sqrt{{\left(\frac{\sqrt{15}}{20}–x\right)}^2+{\left(0,05\right)}^2}}{5}$ (h).

Để thời gian hai bạn di chuyển đến C là bằng nhau thì

$\frac{\sqrt{{\left(\frac{\sqrt{15}}{20}–x\right)}^2+{\left(0,05\right)}^2}}{5}=\frac{x}{15}$

$\iff \sqrt{{\left(\frac{\sqrt{15}}{20}–x\right)}^2+{\left(0,05\right)}^2}=\frac{x}{3}$

Bình phương hai vế của phương trình ta được:

${\left(\frac{\sqrt{15}}{20}–x\right)}^2+{\left(0,05\right)}^2=\frac{x^2}{9}$

$\iff 9\left(\frac{3}{80}–\frac{\sqrt{15}}{10}x+x^2\right)+\frac{9}{400}=x^2$

$\iff 8x^2–\frac{9\sqrt{15}}{10}x+\frac{63}{200}=0$

$\iff \left[\begin{array}{l}x\approx 0,3\\ x\approx 0,1\end{array}\right.$

Vì 0 < x ≤ $\frac{\sqrt{15}}{20}\approx \mathrm{0,19}$ nên $x\approx 0,1$ thỏa mãn.

Vậy hai bạn Minh và Hùng di chuyển đến vị trí C cách điểm B một đoạn khoảng 0,1 km = 100 m.

3. Bài tập tự luyện 

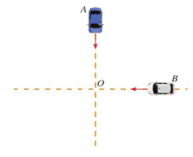
Bài 1. Hai ô tô xuất phát tại cùng một điểm với vận tốc trung bình như nhau là 40 km/h từ hai vị trí A và B trên hai con đường vuông góc với nhau để đi về bến cuối O (Hình vẽ). Vị trí A cách bến 8 km, vị trí B cách bến 7 km. Gọi x là thời gian hai xe bắt đầu chạy cho tới khi cách nhau 5 km. Bạn Dương xác định được x thỏa mãn phương trình $\sqrt{{\left(8–40x\right)}^2+{\left(7–40x\right)}^2}=5.$

Giá trị của x là

A. x ∈ {0,1; 0,275};

B. x ∈ 0,275;

C. x = 0,1;

D. x ∈ Ø.

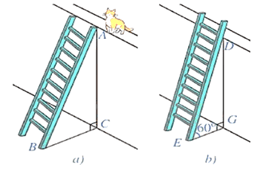
Bài 2. Để leo lên một bức tường, bác Nam dùng một chiếc thang có chiều dài cao hơn bức tường đó 1 m. Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên bức tường (Hình a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m thì bác Nam nhận thấy thang tạo với mặt đất một góc 60° (Hình b).

Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

A. 5;

B. 3,5;

C. 4,7;

D. 4.

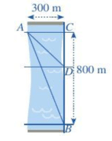
Bài 3. Một người đứng ở điểm A trên bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B cách C một khoảng 800 m (hình vẽ). Vận tốc chèo thuyền là 6 km/h, vận tốc chạy bộ là 10 km/h và giả sử vận tốc dòng nước không đáng kể.

Biết tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút, khoảng cách từ vị trí C đến D là

A. 300 m;

B. 225 m;

C. 250 m;

D. 275 m.

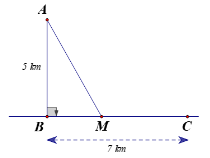
Bài 4. Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng cách AB = 4 km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7 km. Người canh hải đăng có thể chèo thuyền từ A đến vị trí M trên bờ biển với vận tốc 3 km/h rồi đi bộ đến C với vận tốc 5 km/h như hình vẽ.

Biết thời gian người đó đi từ A đến C là 148 phút, khoảng cách từ vị trí B đến M là

A. 4 km;

B. 5 km;

C. 4,5 km;

D. 3 km.

Bài 5. Một ngọn hải đăng đặt ở vị trí A cách bờ biển một khoảng AB = 5 (km). Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7 (km) Người canh hải đăng có thể chèo đò từ A đến vị trí M trên bờ biển với vận tốc 4 (km/h) rồi đi bộ đến C với vận tốc 6 (km/h).

Vị trí của điểm M cách B một khoảng gần nhất với giá trị nào sau đây biết thời gian người đó đi từ A đến C là 135 phút?

A. 1,22 km;

B. 7,0 km;

C. 9,18 km;

D. 1,23 km.

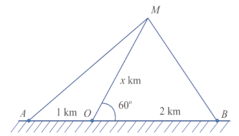
Bài 6. Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc 60°. Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng cách 1 km và 2 km (Hình vẽ).

Đặt độ dài của MO là x. Giá trị của x (làm tròn kết quả đến hàng phần trăm) để khoảng cách từ tàu đến B bằng $\frac{4}{5}$ khoảng cách từ tàu đến A là

A. $x=\frac{11–\sqrt{37}}{3}$;

B. $x=\frac{11\pm \sqrt{37}}{3}$;

C. $x=\frac{11+\sqrt{37}}{3}$;

D. x ∈ Ø.

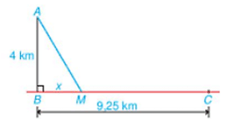
Bài 7. Bác Việt sống và làm việc tại trạm hải đăng cách bờ biển 4 km. Hàng tuần, bác chèo thuyền vào vị trí gần nhất trên bờ biển là bến Bính để nhận hàng hóa do cơ quan cung cấp. Tuần này, do trục trặc về vận chuyển nên toàn bộ số hàng vẫn đang nằm ở thôn Hoành, bên bờ biển cách bến Bính 9,25 km và sẽ được anh Nam vận chuyển trên con đường dọc bờ biển tới bến Bính bằng xe kéo. Bác Việt đã gọi điện thống nhất với anh Nam là họ sẽ gặp nhau ở vị trí nào đó giữa bến Bính và thôn Hoành để hai người có mặt tại đó cùng lúc, không mất thời gian chờ nhau. Giả thiết rằng đường dọc bờ biển là thẳng và bác Việt cũng di chuyển theo một đường thẳng để tới điểm hẹn.

Biết rằng vận tốc của anh Nam là 5 km/h và của bác Việt là 4 km/h. Vị trí hai người hẹn gặp cách bến Bính bao nhiêu km?

A. 6,25;

B. 3;

C. 4;

D. 4,25.

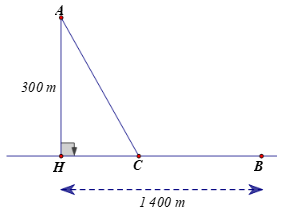
Bài 8. Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6 km/h để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3 km/h. Nếu người chèo thuyền di chuyển theo đường vuông góc với bờ thì phải đi một khoảng cách AH = 300 m và gặp người đi bộ tại địa điểm cách B một khoảng BH = 1 400 m. Tuy nhiên, nếu di chuyển theo cách đó thì hai người không tới cùng lúc. Để hai người đến cùng lúc thì mỗi người người cùng di chuyển về vị trí C (Hình vẽ).

Khoảng cách CB là

A. 400 m;

B. 1 000 m;

C. 1 100 m;

D. 1 700 m.

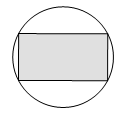
Bài 9. Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50 m (Hình vẽ).

Để tổng quãng đường đi xung quanh vườn hoa đó là 140 m thì diện tích vườn hoa hình chữ nhật là

A. 1 400 m²;

B. 900 m²;

C. 1 200 m²;

D. 1 600 m².

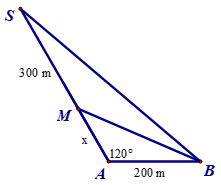
Bài 10. Khoảng cách từ nhà An ở vị trí A đến nhà Bình là 200 m. Từ nhà, nếu An đi x mét theo phương tạo với AB một góc 120° thì sẽ đến nhà bác Mai ở vị trí M và nếu đi thêm 300 m nữa thì sẽ đến siêu thị ở vị trí S.

Biết rằng quãng đường từ nhà Bình đến siêu thị gấp đôi quãng đường từ nhà Bình đến nhà bác Mai. Khi đó quãng đường từ nhà An đến nhà bác Mai là

A. 50 m;

B. 75 m;

C. 100 m;

D. 200 m.