Xét sự biến thiên của hàm số bậc hai (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Xét sự biến thiên của hàm số bậc hai lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Xét sự biến thiên của hàm số bậc hai.

Xét sự biến thiên của hàm số bậc hai (bài tập + lời giải)

1. Phương pháp giải:

Xét hàm số bậc hai y = ax² + bx + c (a ≠ 0), ta có sự biến thiên như sau:

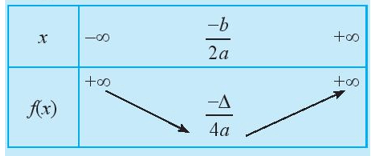
- Với a > 0

+ Hàm số nghịch biến trên khoảng $\left(-\infty ;\frac{-b}{2a}\right)$;

+ Hàm số đồng biến trên khoảng $\left(\frac{-b}{2a};+\infty \right)$;

+ Bảng biến thiên:

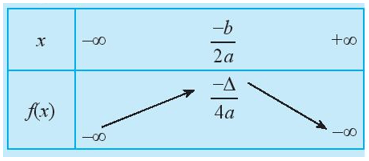
- Với a < 0

+ Hàm số đồng biến trên khoảng $\left(-\infty ;\frac{-b}{2a}\right)$;

+ Hàm số nghịch biến trên khoảng $\left(\frac{-b}{2a};+\infty \right)$;

+ Bảng biến thiên:

2. Ví dụ minh họa.

Ví dụ 1. Xét sự biến thiên và lập bảng biến thiên của hàm số y = –x² + 4x + 5.

Hướng dẫn giải:

Xét hàm số y = –x² + 4x + 5  có a = –1 < 0, b = 4, c = 5

Ta có: $\frac{-b}{2a}=\frac{-4}{2.(-1)}=2$; $-\frac{\Delta }{4a}=-\frac{b^2-4ac}{4a}=-\frac{{\left(-4\right)}^2-4.(-1).5}{4.(-1)}=9$.

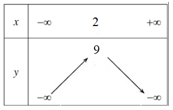
Do đó, hàm số đồng biến trên khoảng (–∞; 2), nghịch biến trên khoảng (2; +∞).

Bảng biến thiên:

Ví dụ 2. Xét sự biến thiên và lập bảng biến thiên của hàm số y = 2x² + 2x + 1.

 Hướng dẫn giải:

Xét hàm số y = 2x² + 2x + 1 có a = 2 > 0, b = 2, c = 1.

Ta có: $\frac{-b}{2a}=\frac{-2}{2.2}=\frac{-1}{2}$; $\frac{-\Delta }{4a}=-\frac{b^2-4ac}{4a}=-\frac{2^2-\mathrm{4.2.1}}{4.2}=\frac{1}{2}$.

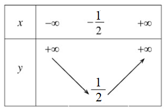
Do đó, hàm số nghịch biến trên khoảng $\left(-\infty ;\frac{-1}{2}\right)$, đồng biến trên khoảng $\left(\frac{-1}{2};+\infty \right)$.

Bảng biến thiên:

3. Bài tập tự luyện.

Bài 1. Hàm số y = x² – 4x + 5 đồng biến trên khoảng:

A. (2; +∞);

B. (–∞; 2);

C. (–2; +∞);

D. (0; +∞).

Bài 2. Hàm số y = –3x² + 6x + 1 đồng biến trên khoảng:

A. (–∞; 2);

B. (2; +∞);

C. (–∞; 1);

D. (1; +∞).

Bài 3. Hàm số y = –x² + 2x – 2 nghịch biến trên khoảng:

A. (–∞; 2);

B. (2; +∞);

C. (–∞; 1);

D. (1; +∞).

Bài 4. Hàm số y = 4x² – 24x – 6 nghịch biến trên khoảng:

A. (–∞; 3);

B. (4; +∞);

C. (–∞; 4);

D. (3; +∞).

Bài 5. Cho hàm số y = x² – 4x – 6. Khẳng định nào sau đây là đúng ?

A. Hàm số đồng biến trên khoảng (–∞; 2);

B. Hàm số đồng biến trên khoảng (–∞; 4);

C. Hàm số nghịch biến trên khoảng (–∞; 2);

D. Hàm số nghịch biến trên khoảng (–∞; 4).

Bài 6. Cho hàm số y = –x² + 8x – 3. Khẳng định nào sau đây là đúng ?

A. Hàm số đồng biến trên khoảng (–∞; 8);

B. Hàm số đồng biến trên khoảng (–∞; 4);

C. Hàm số nghịch biến trên khoảng (–∞; 4);

D. Hàm số nghịch biến trên khoảng (–∞; 8).

Bài 7. Cho hàm số y = –x² + 4x – 3. Khẳng định nào sau đây là đúng ?

A. Hàm số đồng biến trên khoảng (–∞; 2) và nghịch biến trên khoảng (2; +∞);

B. Hàm số nghịch biến trên khoảng (–∞; 2) và đồng biến trên khoảng (2; +∞);

C. Hàm số đồng biến trên khoảng (–∞; 4) và nghịch biến trên khoảng (4; +∞);

D. Hàm số nghịch biến trên khoảng (–∞; 4) và đồng biến trên khoảng (4; +∞).

Bài 8. Cho hàm số y = x² + 6x – 5. Khẳng định nào sau đây là đúng ?

A. Hàm số đồng biến trên khoảng (–∞; 3) và nghịch biến trên khoảng (3; +∞);

B. Hàm số nghịch biến trên khoảng (–∞; –3) và đồng biến trên khoảng (–3; +∞);

C. Hàm số đồng biến trên khoảng (–∞; –3) và nghịch biến trên khoảng (–3; +∞);

D. Hàm số nghịch biến trên khoảng (–∞; 3) và đồng biến trên khoảng (3; +∞).

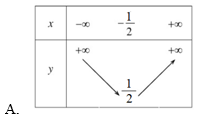
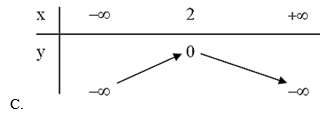
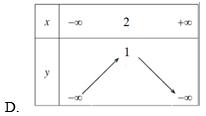
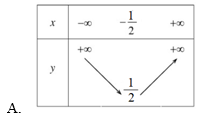
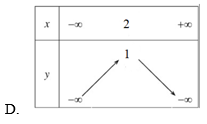
Bài 9. Đâu là bảng biến thiên của hàm số y = –x² + 4x – 3 ?

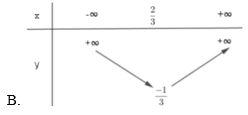
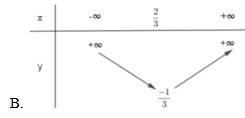
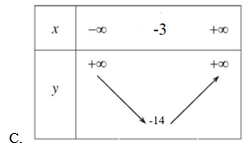
Bài 10. Đâu là bảng biến thiên của hàm số y = x² + 6x – 5 ?