Tìm công thức của hàm số bậc hai khi biết đồ thị hàm số (bài tập + lời giải)

---

Haylamdo sưu tầm bài viết phương pháp giải bài tập Tìm công thức của hàm số bậc hai khi biết đồ thị hàm số lớp 10 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Tìm công thức của hàm số bậc hai khi biết đồ thị hàm số.

Tìm công thức của hàm số bậc hai khi biết đồ thị hàm số (bài tập + lời giải)

1. Phương pháp giải.

* Một số kiến thức cần lưu ý:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = ax² + bx + c (với a ≠ 0) là một parabol (P):

- Có đỉnh S với hoành độ x_S = –$\frac{b}{2a}$, tung độ y_S = –$\frac{\Delta }{4a}$;

- Có trục đối xứng là đường thẳng x = –$\frac{b}{2a}$ (đường thẳng này đi qua đỉnh S và song song với trục Oy nếu b ≠ 0, trùng với trục Oy nếu b = 0);

- Bề lõm quay lên trên nếu a > 0, quay xuống dưới nếu a < 0;

- Cắt trục tung tại điểm có tung độ bằng c, tức là đồ thị đi qua điểm có tọa độ (0; c).

- Nếu b = 2b’ thì (P) có đỉnh S$\left(-\frac{b\text{'}}{a};-\frac{\Delta \text{'}}{a}\right)$;

- Nếu phương trình ax² + bx + c = 0 có hai nghiệm x₁, x₂ thì đồ thị hàm số bậc hai y = ax² + bx + c cắt trục hoành tại hai điểm lần lượt có hoành độ là hai nghiệm này.

* Phương pháp xác định công thức hàm số bậc hai khi biết đồ thị hàm số

Quan sát đồ thị hàm số, xác đinh tọa độ đỉnh, điểm đi qua, trục đối xứng, ... của parabol, từ đó sử dụng các kiến thức tương ứng để xác định hệ số của hàm số, từ đó suy ra công thức hàm số.  

2. Ví dụ minh họa.

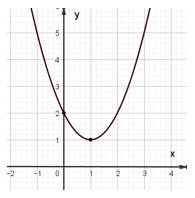
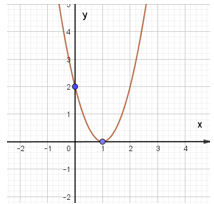
Ví dụ 1: Cho hàm số y = ax²  + bx + c (a ≠ 0) có đồ thị là parabol trong hình dưới. Xác định hàm số đó.

Hướng dẫn giải:

Dựa vào hình vẽ, ta thấy đồ thị hàm số y = ax²  + bx + c có bề lõm hướng lên, đỉnh S(1; 1) và cắt trục tung tại điểm (0; 2).

Do đó ta có:

a > 0 (1)

$-\frac{b}{2a}=1$(2); $-\frac{\Delta }{4a}=1\iff -\frac{b^2-4ac}{4a}=1$(3)

c = 2 (4)

Thay (4) vào (3) ta có: $-\frac{b^2-4a.2}{4a}=1\iff -b^2+8a=4a\iff -b^2+4a=0$(5)

Từ (2) ta có: b = –2a (6)

Thay (6) vào (5) ta có: –(–2a)² + 4a = 0 ⇔ –4a² + 4a = 0

⇔ 4a(–a + 1) = 0 ⇔ $\left[\begin{array}{l}a=0\left(L\right)\\ a=1\left(TM\right)\end{array}\right.$

Với a = 1 ta có: b = –2.1 = –2

Vậy hàm số cần tìm là: y = x²  – 2x + 2.

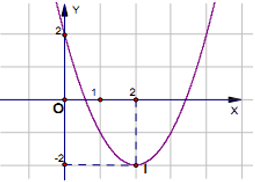
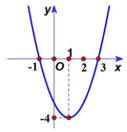
Ví dụ 2: Cho đồ thị hàm số y = ax²  + bx + c (a ≠ 0) trong hình vẽ sau. Xác định hàm số đó. 

Hướng dẫn giải:

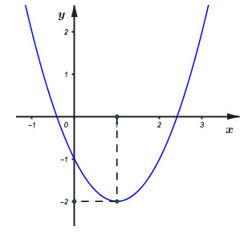
Dựa vào hình vẽ, ta thấy đồ thị hàm số y = ax²  + bx + c có bề lõm hướng lên, đỉnh I(2; –2) và cắt trục tung tại điểm (0; 2).

Do đó ta có:

a > 0 (1)

$-\frac{b}{2a}=2$ (2); $-\frac{\Delta }{4a}=-2\iff -\frac{b^2-4ac}{4a}=-2$(3)

c = 2 (4)

Thay (4) vào (3) ta có: $-\frac{b^2-4a.2}{4a}=-2\iff -b^2+8a=-8a\iff -b^2+16a=0$ (5)

Từ (2) ta có: b = –4a (6)

Thay (6) vào (5) ta có: –(–4a)² + 16a = 0 ⇔ –16a² + 16a = 0

⇔ 16a(–a + 1) = 0 ⇔ $\left[\begin{array}{l}a=0\left(L\right)\\ a=1\left(TM\right)\end{array}\right.$

Với a = 1, ta có: b = –4.1 = –4

Do đó, hàm số cần tìm là: y = x²  – 4x + 2.

3. Bài tập tự luyện.

Bài 1. Đồ thị hàm số trong hình sau là của hàm số bậc hai nào ?

A. y = x²  – 4x + 2;

B. y = –x²  – 4x + 2;

C. y = –x²  + 4x – 4;

D. y = x²  – 4x + 4.

Bài 2. Cho parabol như hình dưới. Xác định hàm số đó.

A. y = 2x²  – 3;

B. y = x²  – 3;

C. y = x²  – 5;

D. y = x²  – 3x.

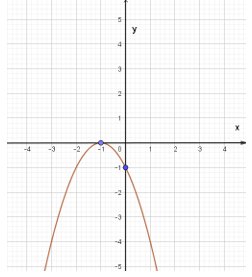
 Bài 3. Đường cong sau đây là đồ thị của hàm số bậc hai nào ?

A. y = x²  – 2x + 1;

B. y = x²  – x – 1;

C. y = x²  – 2x – 1;

D. y = –x²  – 2x – 1.

Bài 4. Cho hàm số y = ax² + bx + c (a ≠ 0) có đồ thị như hình dưới. Xác định hàm số đó.

A. y = x²;

B. y = 2x²;  

C. y = x²  – 5;

D. y = x²  + 4.

Bài 5. Hình vẽ sau là đồ thị của hàm số bậc hai nào ?

A. y = –x²  + 1;

B. y = x²;

C. y = –2x²;  

D. y = –x².

Bài 6. Đồ thị hàm số sau đây là của hàm số bậc hai nào ?

A. y = x²  – 4x + 1;

B. y = x²  – 4x – 2;

C. y = –x²  – 4x;

D. y = x²  – 4x + 3.

Bài 7. Cho hàm số y = ax² + bx + c (a ≠ 0) có đồ thị như hình dưới đây.

Công thức hàm số của đồ thị trên là:

A. y = –x²  – 2x – 1;

B. y = –x²  – 2x + 1;

C. y = x²  – 2x – 1;

D. y = –x²  – 2x.

Bài 8. Cho hàm số bậc hai y = ax² + bx + c (a ≠ 0) có đồ thị như hình dưới.

Khi đó 2a + b + 2c bằng:

A. – 9;

B. 9;

C. – 6;

D. 6.

Bài 9. Cho hàm số bậc hai y = ax² + bx + c (a ≠ 0) có đồ thị như hình dưới.

Xác định công thức của hàm số đó.

A. y = 2x²  – 4x – 2;

B. y = 2x²  – 4x + 2;

C. y = 2x²  – 4x;

D. y = 2x²  + 4x + 2.

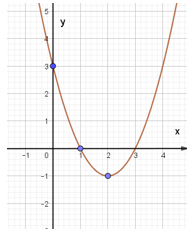
Bài 10. Đồ thị hàm số trong hình sau là của hàm số bậc hai nào ?

A. y = x²  + 4x + 3;

B. y = x²  – 4x + 3;

C. y = x²  – 4x – 3;

D. y = –x²  – 4x + 3.