Biểu diễn góc lượng giác trên đường tròn lượng giác lớp 11 (bài tập + lời giải)

---

Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Biểu diễn góc lượng giác trên đường tròn lượng giác lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Biểu diễn góc lượng giác trên đường tròn lượng giác.

Biểu diễn góc lượng giác trên đường tròn lượng giác lớp 11 (bài tập + lời giải)

1. Phương pháp giải

* Phương pháp:Để biểu diễn góc lượng giác có số đo α trên đường tròn lượnggiác ta cần thực hiện các bước sau:

Bước 1: Vẽ đường tròn lượng giác. Chọn gốc A(1; 0) làm điểm đầu.

Bước 2: Chọn điểm cuối M trên đường tròn lượng giác sao cho (OA, OM) = α.

Điểm cuối M chính là điểm biểu diễn của góc lượng giác có số đo α.

* Một số kiến thức cần lưu ý:

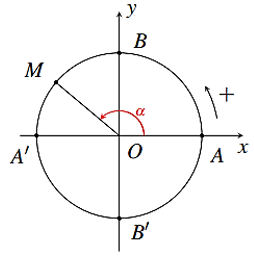
* Đường tròn lượng giác là đường tròn có tâm tại gốc tọa độ, bán kính bằng 1, được định hướng với chiều quay dương (ngược chiều quay của kim đồng hồ), chiều quay âm (cùng chiều quay của kim đồng hồ) và lấy điểm A(1; 0) làm điểm gốc của đường tròn.

Các điểm B(0; 1), A(– 1; 0), B'(0; – 1) nằm trên đường tròn lượng giác.

* Nếu |α| > 2π (hoặc |α| > 360°)ta phân tích α = β + k2π (hoặc α = β + k360°) với – π< β < π. Khi đó, điểm biểu diễn của góc lượng giác có số đo α sẽ trùng với điểm biểu diễn của góc lượng giác có số đo là β.

* α > 0 thì góc α quay theo chiều dương, α < 0 thì góc α quay theo chiều âm.

2. Ví dụ minh họa

Ví dụ 1. Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng 45°.

Hướng dẫn giải

Ta có (OA, OM) = 45° là góc lượng giác có tia đầu là tia OA, tia cuối là tia OM và quay theo chiều dương (ngược chiều quay của kim đồng hồ) một góc 45°.

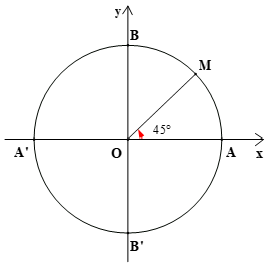
Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng 45° được xác định như hình dưới đây:

Vậy điểm M là điểm chính giữa của cung nhỏ

Ví dụ 2. Xác định điểm N trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng $-\frac{9\pi }{4}.$

Hướng dẫn giải

Vì (OA, ON) = $-\frac{9\pi }{4}=-\frac{\pi }{4}+\left(-1\right).2\pi$, do vậy điểm N trùng với điểm biểu diễn của góc lượng giác có số đo bằng $-\frac{\pi }{4}.$

Khi đó, góc (OA, ON) là góc lượng giác có tia đầu là tia OA, tia cuối là tia ON và quay theo chiều âm (cùng chiều quay của kim đồng hồ) một góc $\frac{\pi }{4}.$

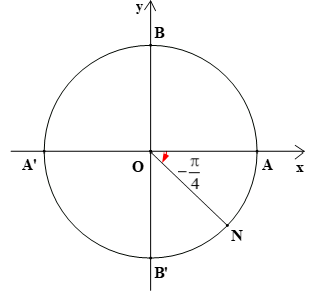
Điểm N trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng $-\frac{9\pi }{4}$ được biểu diễn như hình dưới đây:

Vậy điểm N là điểm chính giữa của cung nhỏ $\stackrel{⏜}{B^{\text{'}}A}.$

3. Bài tập tự luyện

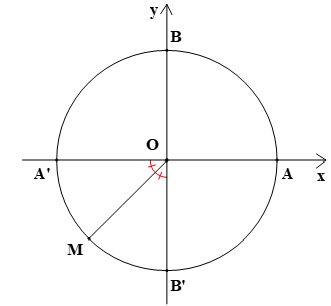
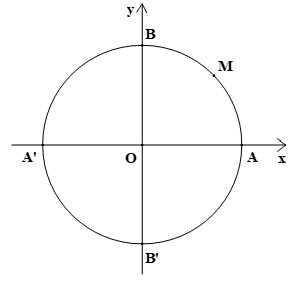
Bài 1. Số đo của các góc lượng giác (OA, OM) trong hình vẽ dưới đây là:

A.$\frac{3\pi }{4}$ + k2π, k ∈ ℤ;

B. $\frac{-3\pi }{4}$+ k2π, k ∈ ℤ;

C. $\frac{3\pi }{4}$+ kπ, k ∈ ℤ;

D. $\frac{-3\pi }{4}$+ kπ, k ∈ ℤ.

Bài 2. Khi biểu diễn góc lượng giác trên đường tròn lượng giác, khẳng định nào sau đây là sai?

A. Điểm biểu diễn góc α và góc π – α đối xứng nhau qua trục tung;

B. Điểm biểu diễn góc α và góc – α đối xứng qua gốc tọa độ;

C. Mỗi góc lượng giác được biểu diễn bởi một điểm duy nhất;

D. Góc α và góc α + k2π (k ∈ ℤ) có cùng điểm biểu diễn.

Bài 3. Điểm biểu diễn góc lượng giác có số đo bằng $\frac{9\pi }{4}$ là điểm nào trong hình vẽ dưới đây?

A. Điểm A;

B. Điểm B';

C. Điểm M;

D. Điểm B.

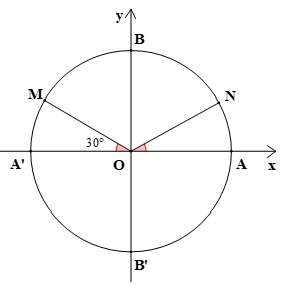
Bài 4. Điểm biểu diễn góc lượng giác có số đo bằng $-\frac{7\pi }{6}$ là điểm nào trong hình vẽ dưới đây?

A. Điểm A;

B. Điểm N;

C. Điểm M;

D. Điểm A'.

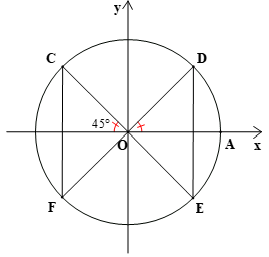
Bài 5. Cho hình vẽ dưới đây:

Mệnh đề nào sau đây là đúng?

A. Điểm C biểu diễn góc $-\frac{5\pi }{4}$ ;

B. Điểm D biểu diễn góc  $\frac{-\pi }{4}$;

C. Điểm F biểu diễn góc $\frac{3\pi }{4}$;

D. Điểm E biểu diễn góc $\frac{\pi }{4}$ .

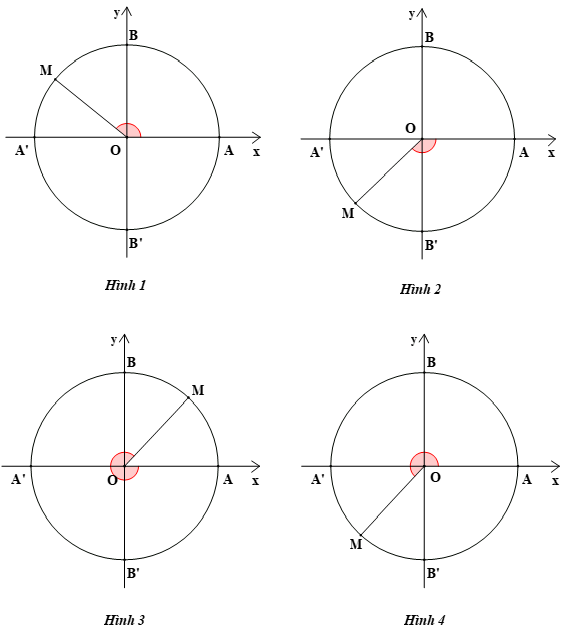
Bài 6. Hình biểu diễn góc lượng giác (OA, OM) = – 135° là

A. Hình 1;

B. Hình 2;

C. Hình 3;

D. Hình 4.

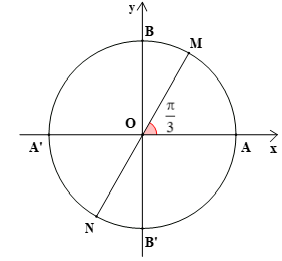
Bài 7. Trên hình vẽ, hai điểm M, N biểu diễn các góc lượng giác có số đo là:

A.  $\frac{\pi }{3}$+ k2π, k ∈ ℤ;

B.  $\frac{-\pi }{3}$+ $\frac{-\pi }{3}$k2π, k ∈ ℤ;

C.  $\frac{\pi }{3}$+ kπ, k ∈ ℤ;

D. $\frac{\pi }{3}$ + k $\frac{\pi }{2}$, k ∈ ℤ.

Bài 8. Trên đường tròn lượng giác gốc A, lấy điểm M sao cho góc lượng giác (OA, OM) = . Gọi M₁ là điểm đối xứng với M qua Ox. Số đo của các góc lượng giác (OA, OM₁) là:

A. $\frac{-5\pi }{3}$ + k2π, k ∈ ℤ;

B. $\frac{\pi }{3}$ + k2π, k ∈ ℤ;

C. $\frac{-\pi }{3}$ + k2π, k ∈ ℤ;

D. $\frac{-\pi }{3}$ + kπ, k ∈ ℤ.

Bài 9. Số điểm M trên đường tròn lượng giác biểu diễn các góc lượng giác có số đo bằng $\frac{\pi }{6}+\frac{k2\pi }{3}$, k ∈ ℤ là

A. 6;

B. 4;

C. 3;

D. 8.

Bài 10. Trên đường tròn với điểm gốc là A. Điểm M thuộc đường tròn sao cho $\widehat{AOM}=60°.$  Gọi N là điểm đối xứng với M qua trục Oy, số đo của các góc lượng giác (OA, ON) là

A. – 120° hoặc 240°;

B. 120° + k360°, k ∈ ℤ;

C. 60° + k360°, k ∈ ℤ;

D. 120° + k180°, k ∈ ℤ.