Các bài toán về tính chất của hình lăng trụ và hình hộp lớp 11 (bài tập + lời giải)
Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Các bài toán về tính chất của hình lăng trụ và hình hộp lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Các bài toán về tính chất của hình lăng trụ và hình hộp.
Các bài toán về tính chất của hình lăng trụ và hình hộp lớp 11 (bài tập + lời giải)
1. Phương pháp giải
- Hình lăng trụ có hai mặt đáy là hai đa giác lồi nằm trên hai mặt phẳng song song và các cạnh bên là các đường thẳng song song.
- Hình lăng trụ có hai đáy là hình bình hành được gọi là hình hộp.
- Các tính chất của hình lăng trụ:
+ Hai mặt đáy của hình lăng trụ song song với nhau.
+ Các cạnh bên của hình lăng trụ song song với nhau.
+ Các mặt bên của hình lăng trụ là hình bình hành.
- Các tính chất của hình hộp:
+ Các mặt đối diện của hình hộp song song với nhau.
+ Các mặt của hình hộp đều là hình bình hành.
+ Các đường chéo của hình hộp cắt nhau tại trung điểm của mỗi đường.
2. Ví dụ minh họa:
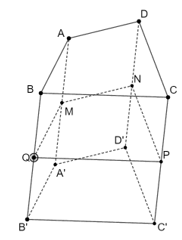
Ví dụ 1. Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Mặt phẳng (P) song song với mặt đáy của hình lăng trụ và cắt các cạnh bên của hình lăng trụ tại M, N, P, Q. Chứng mình rằng ABCD.MNPQ là hình lăng trụ.
Hướng dẫn giải:
Vì M, N, P, Q nằm trên các cạnh bên của hình lăng trụ, mà các cạnh bên của các hình lăng trụ song song với nhau nên AM // BN // CP // DQ.
Hơn nữa (ABCD) và (MNPQ) song song với nhau nên ABCD.MNPQ là hình lăng trụ tứ giác.
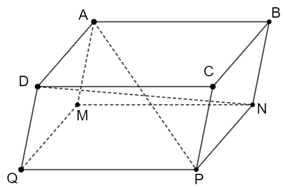
Ví dụ 2. Cho hình hộp ABCD.MNPQ. Chứng minh rằng các đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường.
Hướng dẫn giải:
Vì đáy của hình hộp là hình bình hành nên AD // BC và AD = BC.
Mặt bên BCPN là hình bình hành nên BC // NP và BC = NP.
Suy ra AD // NP và AD = NP, từ đó ta được ADPN là hình bình hành.
Vậy AP và ND cắt nhau tại trung điểm mỗi đường.
Tương tự ta được BQ và AP cắt nhau tại trung điểm mỗi đường.
Vậy các đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường.
3. Bài tập tự luyện
Bài 1. Hai mặt đáy của hình lăng trụ
A. Song song với nhau;
B. Hợp với nhau một góc 15o;
C. Hợp với nhau một góc 30o;
D. Hợp với nhau một góc 45o.
Bài 2. Các cạnh bên của hình lăng trụ
A. Có độ dài bằng nhau;
B. Song song với nhau;
C. A và B đều đúng;
D. Một đáp án khác.
Bài 3. Các mặt bên của hình lăng trụ là
A. Hình thoi;
B. Hình vuông;
C. Hình chữ nhật;
D. Hình bình hành.
Bài 4. Khẳng định nào sau đây là đúng
A. Các mặt đối diện của hình hộp song song với nhau;
B. Các cạnh bên của hình hộp song song với nhau;
C. Hình hộp có 8 đỉnh;
D. Cả 3 đáp án đều đúng.
Bài 5. Các mặt của hình hộp là
A. Hình vuông;
B. Hình chữ nhật;
C. Hình bình hành;
D. Hình tứ giác.
Bài 6. Các đường chéo của hình hộp
A. Tạo thành một tam giác đều;
B. Tạo thành một tam giác cân;
C. Tạo thành một tam giác;
D. Đồng quy tại trung điểm mỗi đường.
Bài 7. Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Khi đó ABCD.MNPQ là hình gì?
A. Hình hộp;
B. Hình hộp chữ nhật;
C. Hình lập phương;
D. Hình lăng trụ tứ giác.
Bài 8. Cho hình lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của các cạnh AB, A’B’. MNC’C là
A. Hình tứ giác;
B. Hình chữ nhật;
C. Hình bình hành;
D. Hình thoi.
Bài 9. Cho hình lăng trụ ABC.A’B’C’. Gọi G là trọng tâm của các tam giác ABC. Lấy điểm M trên cạnh AC sao cho AM = 2MC. Vị trí tương đối của GM và (BCC’B’) là
A. Song song với nhau;
B. Cắt nhau;
C. GM nằm trên (BCC’B’);
D. Không xác định được.
Bài 10. Cho hình hộp ABCD.A’B’C’D’. Gọi giao điểm của AC và BD là O; giao điểm của A’C’ và B’D’ là O’. Vị trí tương đối của (O’AB) và (OC’D’) là
A. Cắt nhau;
B. Song song với nhau;
C. Trùng nhau;
D. Không xác định được.