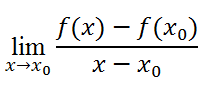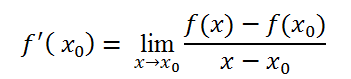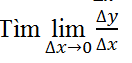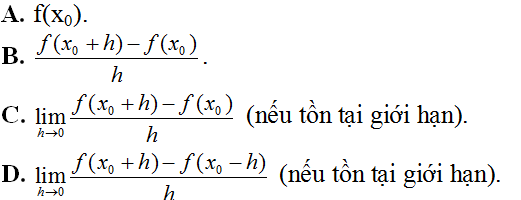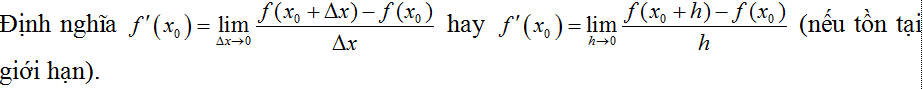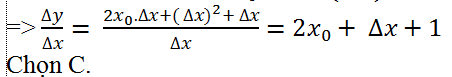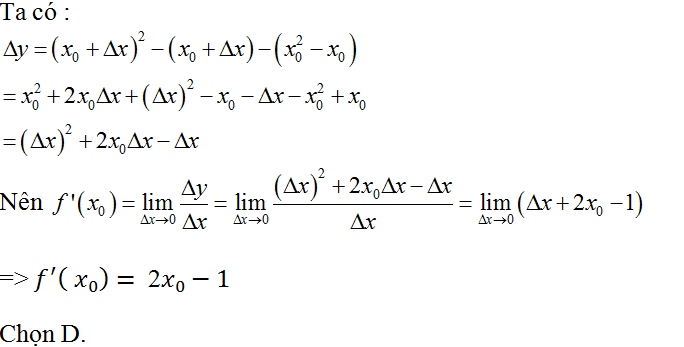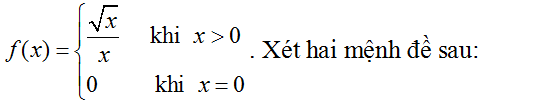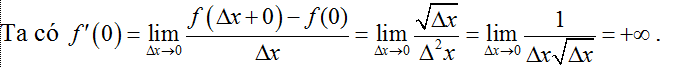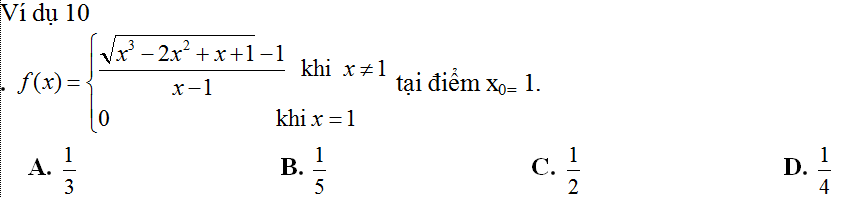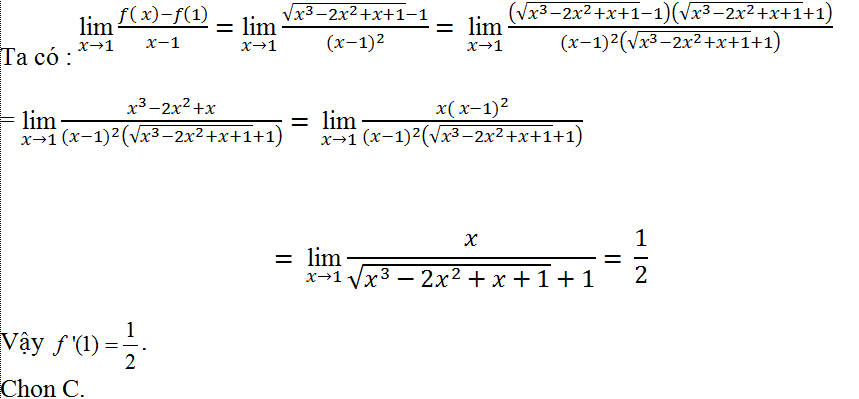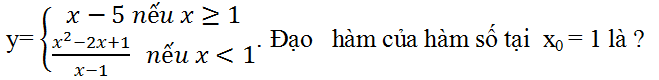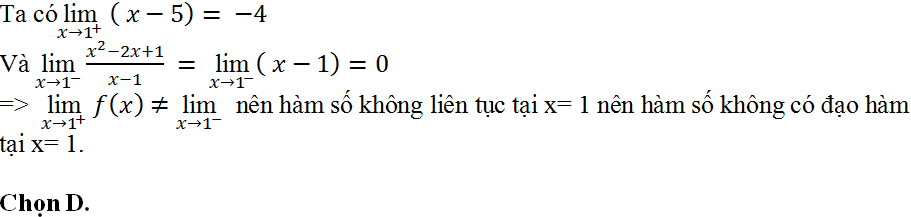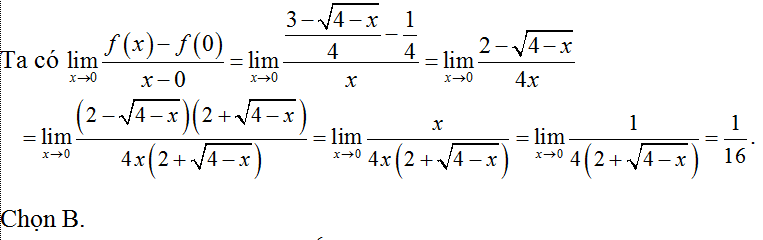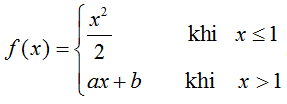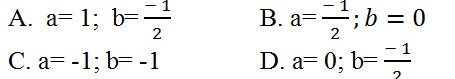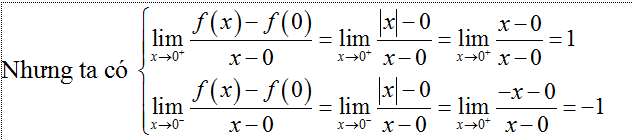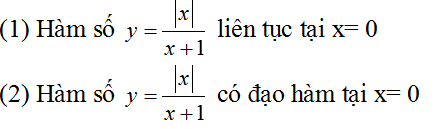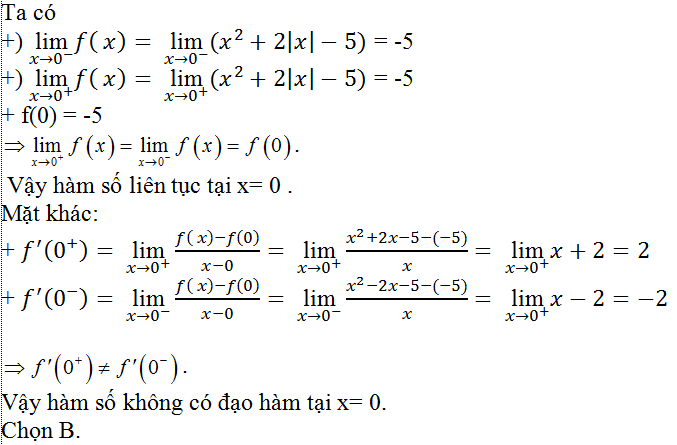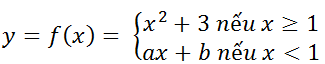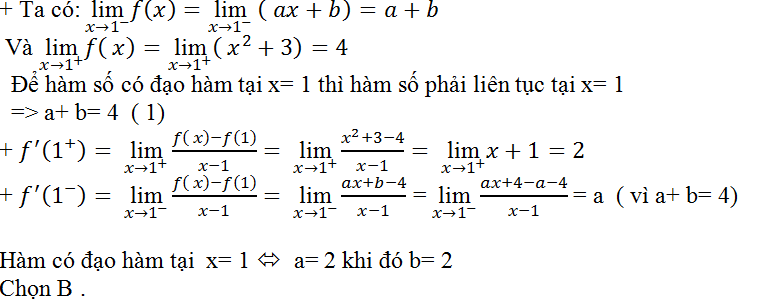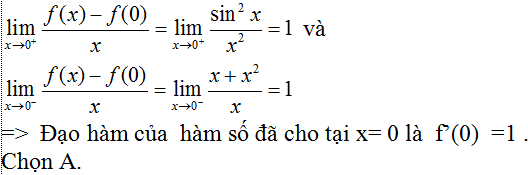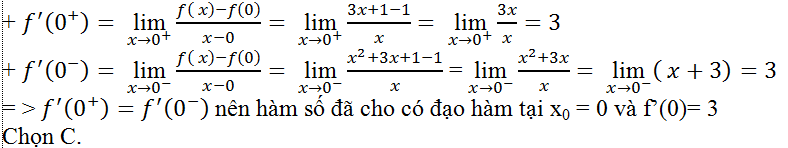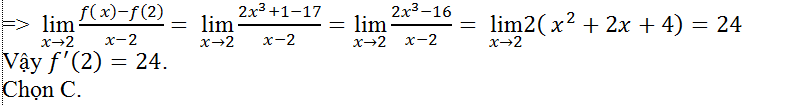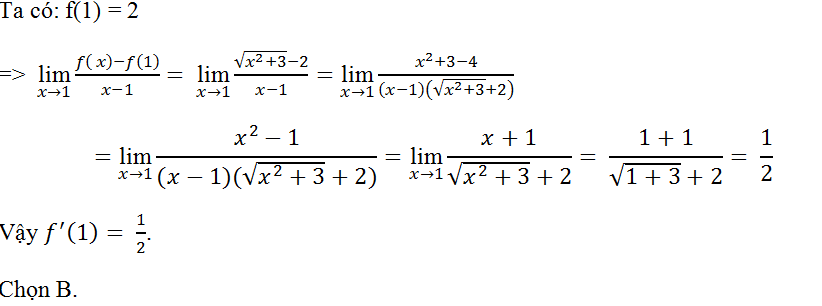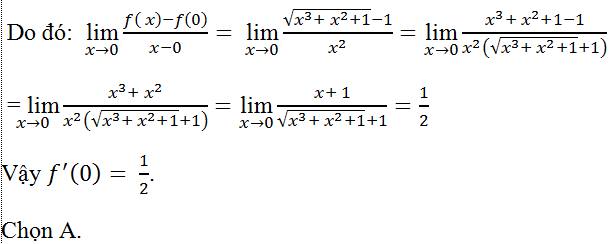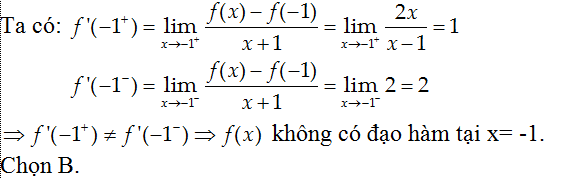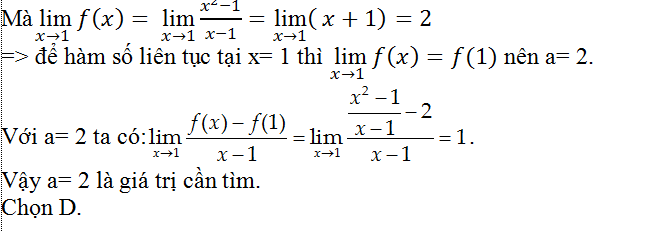Bài tập tính đạo hàm bằng định nghĩa cực hay, có lời giải - Toán lớp 11
Bài tập tính đạo hàm bằng định nghĩa cực hay, có lời giải
Với Bài tập tính đạo hàm bằng định nghĩa cực hay, có lời giải Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính đạo hàm bằng định nghĩa từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải
+ Định nghĩa đạo hàm của hàm số: Cho hàm số y= f(x) xác định trên khoảng (a; b) và x0∈(a;b). Nếu tồn tại giới hạn hữu hạn:
Thì giới hạn đó được gọi là đạo hàm của hàm số y= f( x) tại điểm x0 và kí hiệu:
+ Quy tắc tính đạo hàm bằng định nghĩa:
Bước 1: giả sử ∆ x là số gia của đối số x0. Tính ∆ y= f(x0 + ∆x) – f(x0) .
Bước 2: Lập tỉ số ∆y/∆x
Bước 3.
B. Ví dụ minh họa
Ví dụ 1. Giới hạn (nếu tồn tại) nào sau đây dùng để định nghĩa đạo hàm của hàm số y= f(x) tại x0 < 1 ?
Hướng dẫn giải
Theo định nghĩa đạo hàm của hàm số tại một điểm thì biểu thức ở đáp án C đúng.
Chọn C.
Ví dụ 2. Cho hàm số y= f(x) liên tục tại x0. Đạo hàm của hàm số y= f(x) tại x0 là
Hướng dẫn giải
Chọn C.
Ví dụ 3. Số gia của hàm số y= f(x )= x3 + 1 ứng với x0= 1 và ∆ x= 1 bằng bao nhiêu?
A. – 10 B . 7 C. - 1. D. 0
Hướng dẫn giải
Ta có ∆y= f( x0+ ∆x)-f(x0 )=( x0+ ∆x)3+1- x03-1
= 3.x02.∆x+3x0 ( ∆x)2+( ∆x)3
Với x0 =1 và ∆ x=1 thì ∆ y=7.
Chọn B
Ví dụ 4 . Tỉ số ∆y/∆x của hàm số f(x) = x2+ x theo x và là
A. 2x02 ∆x+1 B. 2x0- ∆x
C. 2x0+ ∆x+1 D. 2x0.∆x+(∆x)2+1
Hướng dẫn giải
Giả sử ∆x là số gia của đối số tại xo . Ta có:
∆ y=f( x0+ ∆x)-f( x0 )=( x0+ ∆x)2+ x0+ ∆x- x02- x0
= x02+ 2x0.∆x+( ∆x)2+ x0+ ∆x- x02- x0
= 2x0.∆x+( ∆x)2+ ∆x
Ví dụ 5. Số gia của hàm số y= f( x) = 2x+ 8 ứng với số gia của đối số x tại x0= 3 là
A. 3 B. 2∆x C. -2∆x + 3 D. Đáp án khác
Hướng dẫn giải
Với số gia của đối số x tại x0 = 3. Ta có
∆ y=f( x0+ ∆x)-f( x0 )=2( x0+ ∆x)+8-2x0-8 = 2∆x
suy ra Số gia của hàm số tại x0 = 3 là 2∆x.
Chọn B

Ví dụ 6. Cho hàm số y= x3- 1. Tính ∆ y của hàm số theo x và ∆ x?
A. 3x2.∆ x+ 3x. (∆x)2+( ∆x)3
B. x2.∆ x+ x. (∆x)2+( ∆x)3
C. 3x2.∆ x+ 3x.(∆x)2+( ∆x)3 +2
D. Đáp án khác
Hướng dẫn giải
+ Giả sử ∆ x là số gia của đối số.
+ Ta có; ∆y= f( x+∆x) - f( x) = (x+∆x)3 – 1- x3+1
= x3+ 3x2.∆ x+ 3x. (∆x)2+( ∆x)3 – x3
= 3x2.∆ x+ 3x. (∆x)2+( ∆x)3
Chọn A.
Ví dụ 7. Cho hàm số y= x2+ 2x- 3. Tính tỉ số ∆y/∆x theo x và ∆ x
A. 2x+ ∆x-2 B. 2x+ ∆x+2(∆)2
C. 2x- ∆x+2 D. 2x+ ∆x+2
Hướng dẫn giải
+ Gọi ∆x là số gia của đối số x.
+ Ta có: ∆ y= f(x+ ∆x) – f(x)= [(x+∆x)2 +2(x+ ∆x)- 3] – [x2+ 2x -3]
= x2+ 2x. ∆x + (∆x)2+ 2x +2.∆x – 3 – x2- 2x + 3
= 2x. ∆x + ( ∆x)2+ 2.∆x
+ ∆y/∆x=2x+ ∆x+2
Chọn D.
Ví dụ 8. Cho hàm số y= f( x)= x2- x, đạo hàm của hàm số ứng với số gia của đối số x tại x0 là
A.x0+1 B. x0 – 2 C. x0 - 2∆x D. 2x0 - 1
Hướng dẫn giải
Ví dụ 9. Cho hàm số
(I). f' (0)=1
(II) Hàm số không có đạo hàm tại x0= 0.
Mệnh đề nào đúng?
A. Chỉ (I). B. Chỉ (II). C. Cả hai đều sai. D. Cả hai đều đúng.
Hướng dẫn giải
Gọi ∆x là số gia của đối số tại 0 sao cho ∆ x > 0 .
Nên hàm số không có đạo hàm tại 0.
Chọn B.
Ví dụ 10.
Hướng dẫn giải
Ví dụ 11. Cho hàm số y= 8x+ 10. Tính đạo hàm của hàm số tại x0= -1.
A. 6 B. 10 C. 8 D. - 15
Hướng dẫn giải
+ Giả sử ∆x là số gia của đối số tại x0= -1.
∆ y= f( -1+ ∆x) – f( -1) = 8( - 1+∆x)+ 10 –[ 8.(- 1)+ 10]
= - 8+ 8∆x+ 10- 2 = 8.∆x
suy ra ∆y/∆x=8 nên
Vậy đạo hàm của hàm số đã cho tại điểm x0= -1 là 8.
Chọn C.
Ví dụ 12. Cho hàm số:
A. 0 B. 2 C. 1 D. Đáp án khác
Hướng dẫn giải
Ví dụ 13. Cho hàm số
Hướng dẫn giải
Ví dụ 14. Cho hàm số
Với giá trị nào của a; b thì hàm số có đạo hàm tại x= 1?
Hướng dẫn giải

C. Bài tập vận dụng
Câu 1: Số gia của hàm số y= - 3x2+ 8 ứng với x và là
A. -6x. ∆x -3(∆x)2 B. -6x. ∆x+ 3(∆x)2- 16
C. 6x. ∆x -3(∆x)2 + 16 D. -6x - 3. ∆x
Lời giải:
+ Gọi ∆x là số gia của đối số x.
+ Ta có: ∆ y= f(x+ ∆x) – f(x)= [ - 3(x+∆x)2 +8] – [- 3x2+ 8]
= -3x2 - 6x. ∆x -3(∆x)2+ 8 + 3x2- 8
= -6x. ∆x -3(∆x)2
Chọn A.
Câu 2: Xét ba mệnh đề sau:
(1) Nếu hàm số y= f(x) có đạo hàm tại điểm x= x0 thì hàm số liên tục tại điểm đó.
(2) Nếu hàm số y= f( x) liên tục tại điểm x= x0 thì hàm số y= f(x) có đạo hàm tại điểm đó.
(3) Nếu y=f(x) gián đoạn tại x= x0 thì chắc chắn hàm số y=f(x) không có đạo hàm tại điểm đó.
Trong ba câu trên:
A. Có hai câu đúng và một câu sai. B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng. D. Cả ba đều sai.
Lời giải:
(1) Nếu hàm số y=f(x) có đạo hàm tại điểm x= x0 thì hàm số y= f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số y= f(x) liên tục tại điểm x= x0 thì hàm số y=f(x) có đạo hàm tại điểm đó là mệnh đề sai.
Ví dụ : Lấy hàm ta có D= R nên hàm số y= f(x) liên tục trên R .
Nên hàm số không có đạo hàm tại x= 0.
(3) Nếu hàm số y= f(x) gián đoạn tại x=x0 thì chắc chắn hàm không có đạo hàm tại điểm đó là mệnh đề đúng.
Vì (1) là mệnh đề đúng nên (1) tương đương với mệnh đề sau: Nếu hàm số y=f( x) không liên tục tại x= x0 thì hàm số y= f(x) không có đạo hàm tại điểm đó.
Vậy (3) là mệnh đề đúng.
Chọn A.
Câu 3: Xét hai câu sau:
Trong hai câu trên:
A. Chỉ có (2) đúng. B. Chỉ có (1) đúng. C. Cả hai đều đúng. D. Cả hai đều sai.
Lời giải:
Câu 4: Cho hàm số y= x2+2|x|-5. Xét hai câu sau:
(1). Hàm số trên có đạo hàm tại x= 0.
(2). Hàm số trên liên tục tại x= 0.
Trong hai câu trên:
A. Chỉ có (1) đúng. B. Chỉ có (2) đúng. C. Cả hai đều đúng. D. Cả hai đều sai.
Lời giải:
Câu 5: Tìm a; b để hàm số
có đạo hàm tại x= 1.
A. a= - 3; b= 7 B. a= 2; b=2 C. a= 1;b= 3 D. a= 4; b= 0
Lời giải:

Câu 6: Cho hàm số 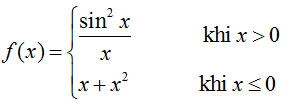
A. 1 B. 2 C. 3 D. 5
Lời giải:
Ta có: f(0) = 0. Xét các đạo hàm một bên của hàm số:
Câu 7: Tính đạo hàm của hàm số 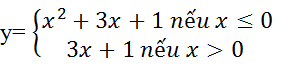
A. 2 B. 0 C. 3 D. đáp án khác
Lời giải:
Ta có: f(0) = 1. Ta xét các đạo hàm một bên của hàm số:
Câu 8: Tính đạo hàm của hàm số y= f(x)= 2x3 +1 tại các điểm x= 2.
A. 12 B. 16 C. 24 D. 18
Lời giải:
Ta có: f(2) = 2.23+ 1= 17
Câu 9: Tính đạo hàm của hàm số y= f(x)= √(x2+3) tại x= 1
A.1 B. 1/2 C. 2 D. 1/4
Lời giải:
Câu 10: Tính đạo hàm của hàm số 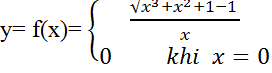
A. 1/2 B.1 C. 2 D. 1/4
Lời giải:
Ta có f(0) = 0
Câu 11: Cho hàm số y= f(x)= (2x2+ |x+1|)/(x-1). Tìm mệnh đề đúng?
A. Hàm số đã cho có đạo hàm tại x= -1.
B. Hàm số đã cho liên tục nhưng không có đạo hàm tại x= -1.
C. Hàm số đã cho không liên tục tại x= -1
D. Hàm số đã cho có đạo hàm tại x= -1 nhưng không liên tục tại điểm đó.
Lời giải:
Vì hàm số y= f(x) xác định tại x= -1 nên nó liên tục tại đó.
Câu 12: Tìm a để hàm số 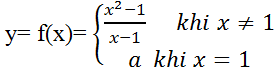
A. – 1 B. 1 B. – 2 D. 2
Lời giải:
Để hàm số có đạo hàm tại x= 1 thì trước hết hàm số phải liên tục tại x= 1
Câu 13: Tính đạo hàm của hàm số 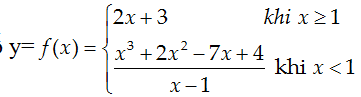
A. 0 B. 4 C. 5 D. Đáp án khác
Lời giải: