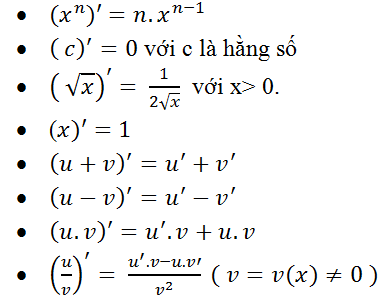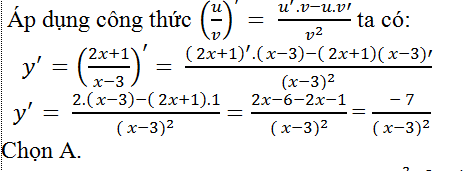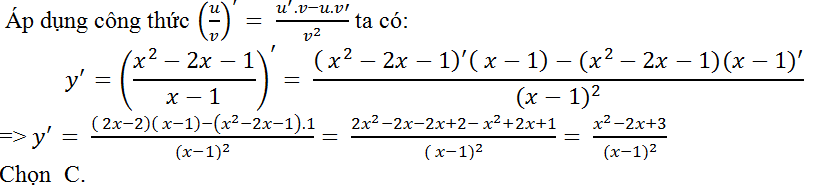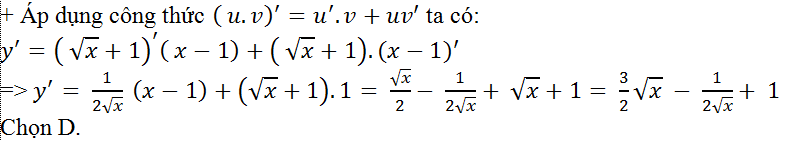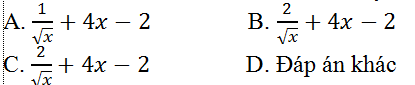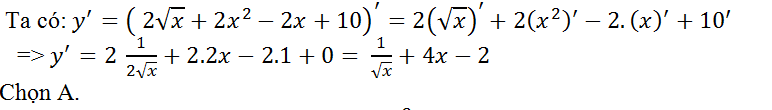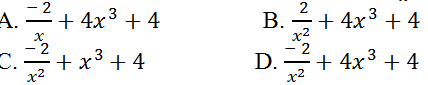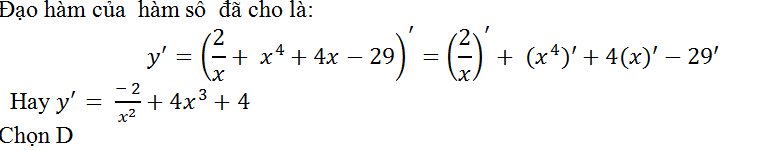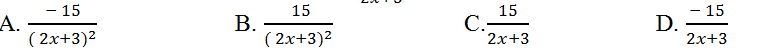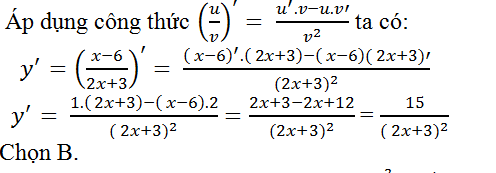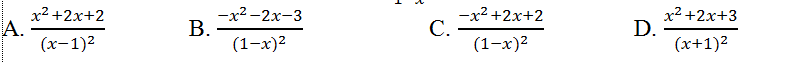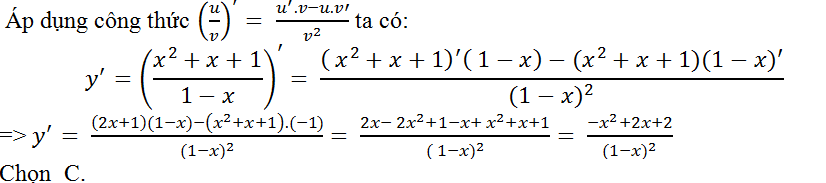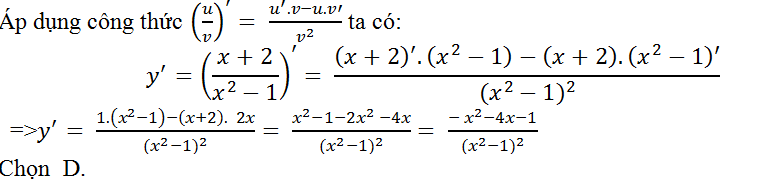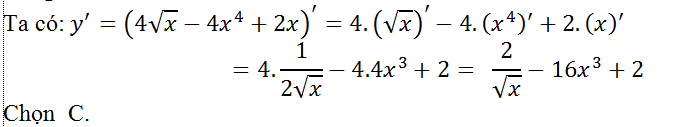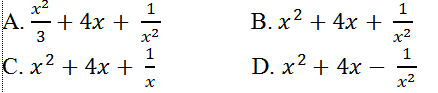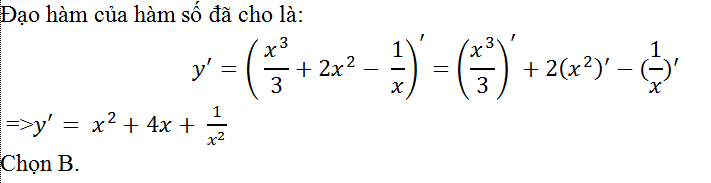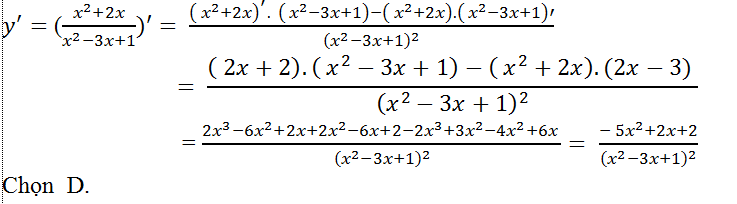Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết - Toán lớp 11

---

Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết

Với Cách tính đạo hàm của các hàm số đơn giản hay, chi tiết Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính đạo hàm của các hàm số đơn giản từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

Đạo hàm của các hàm số cơ bản :

Trong đó u= u(x) ; v= v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định.

B. Ví dụ minh họa

Ví dụ 1. Đạo hàm của hàm số y= 2017 là

A. 2017       B. -2017       C. 0       D. 1

Hướng dẫn giải

Hàm số y= 2017 là hàm hằng nên y'=0

Chọn C

Ví dụ 2. Cho hàm số y= f(x) = 27- 27x. Trong các mệnh đề sau, mệnh đề nào đúng?

A.f' (x)=27        B. f'(x)= - 27       C. f' (x)=27x       D. f' (x)=1-27x

Hướng dẫn giải

Ta có: f' (x)=( 27-27x)'=(27)'-( 27x)'=0-27= -27

Chọn B.

Ví dụ 3. Cho hàm số y= 2x²+ 2x- 10. Tính đạo hàm của hàm số đã cho

A. 4x+ 2        B. 4x- 10

C. 2x+ 2        D. không tồn tại.

Hướng dẫn giải

Ta có: f' (x)=( 2x²+2x-10)'=2(x² )'+2.x'-(10)'=2.2x+2.1-0

⇒ f’(x)= 4x+ 2

Chọn A

Ví dụ 4. Đạo hàm của hàm số y= f(x)= x⁵ – 3x²+ 6x -10 là

A. x⁵- 6x + 6 B. x⁴- x²+ 6

C. 5x⁴ – 3x + 6 D. 5x⁴- 6x+ 6

Hướng dẫn giải

Ta có: f' (x)=(x⁵-3x²+6x-10)'=(x⁵ )'-3(x² )'+6.(x)'-(10)'

⇒f’(x)= 5x⁴ – 6x + 6

Chọn D.

Ví dụ 5. Đạo hàm của hàm số y= f(x)= (x+1)( 3- 2x) bằng biểu thức nào sau đây?

A. 3x- 2        B. 1- 4x       C. 2- 4x        D. 1+ 2x

Hướng dẫn giải

Áp dụng công thức: (u.v)'=u'.v+u.v' ta có:

f' (x)=( x+1)'.( 3-2x)+( x+1).(3-2x)'

⇒ f'(x)= 1.( 3-2x)+ (x+1). (-2) = 3- 2x- 2x- 2= 1- 4x

Chọn B.

Ví dụ 6. Đạo hàm của hàm số y=f(x)= ( x- 1)²( x- 3) bằng biểu thức nào?

A. 2x³- 2x+ 1        B.3x²- 10x + 7

C.2x²+ 5x – 7        D. 4x² – 2x + 8

Hướng dẫn giải

+ Áp dụng công thức: (u.v)'=u'.v+u.v' ta có:

⇒ f' (x)=[ (x-1)² ]'.( x-3)+(x-1)² (x-3)'

= 2(x-1) (x-3) + (x-1)². 1 = 2(x² – 3x- x + 3) + x² – 2x+ 1

= 2x²- 6x – 2x+ 6+ x² – 2x + 1 = 3x² – 10x + 7

Chọn B.

Ví dụ 7. Tính đạo hàm của hàm số y= (2x+1)/(x-3)?

Hướng dẫn giải

Ví dụ 8. Tính đạo hàm của hàm số y= (x²-2x-1)/(x-1)?

Hướng dẫn giải

Ví dụ 9. Tính đạo hàm của hàm số: y=2√x + 2x²- 1?

A. 1/√x+4x        B. 2 1/√x+4x-2        C. 1/(2√x)+4x        D. Tất cả sai

Hướng dẫn giải

Ta có: y'=(2√x+2x²-1)'=2.(√x)'+2.(x² )'-(1)'

=2.1/(2√x)+2.2x-0= 1/√x+4x

Chọn A.

Ví dụ 10. Tính đạo hàm của hàm số: y=(√x+1).( x-1)

Hướng dẫn giải

Ví dụ 11. Tính đạo hàm của hàm số: y= 2√x + 2x² – 2x+ 10

Hướng dẫn giải

Ví dụ 12. Tính đạo hàm của hàm số y= 2/x+ x⁴+4x-29

Hướng dẫn giải

C. Bài tập vận dụng

Câu 1: Đạo hàm của hàm số y= - 18√2 là:

A . - 18        B. 18        C. - 18√2        D. 0

Lời giải:

Hàm số y= - 18√2 là hàm hằng nên y'=0

Chọn D.

Câu 2: Cho hàm số y= f(x) = - 2x + 10. Trong các mệnh đề sau, mệnh đề nào đúng?

A.f' (x)=2        B. f'(x)= - 2       C. f' (x)=10       D. f' (x)=-10

Lời giải:

Ta có: f' (x)=(-2x+10)'=(-2x)'+( 10)'=-2-0= -2

Chọn B.

Câu 3: Cho hàm số y= -x² - 7x + 8. Tính đạo hàm của hàm số đã cho

A. –x- 7        B. 2x + 7

C. 2x - 7       D. -2x- 7

Lời giải:

Ta có: f' (x)=(-x²-7x+8)'=-(x )'-7.(x)'+(8)'=-2x-7.1+0

⇒ f’(x)= -2x - 7

Chọn D.

Câu 4: Đạo hàm của hàm số y= f(x)= 2x⁴ + 2x² + x + 28 là

A. 8x³ +2x + 1        B. 8x³ +4x+ 1

C. 8x⁴ + 4x + 1        D. 4x³ +2x+ 1

Lời giải:

Ta có: f' (x)=(2x⁴+2x²+x+28)'=2(x⁴ )'+2(x² )'+(x)'+(28)'

⇒f’(x)= 8x³ +4x + 1

Chọn B.

Câu 5: Đạo hàm của hàm số y= f(x)= (x- 6)(8- 4x) bằng biểu thức nào sau đây?

A. 32- 8x        B. 6x- 24       C. - 4x + 32       D. 2x+ 16

Lời giải:

Áp dụng công thức: (u.v)'=u'.v+u.v' ta có:

f' (x)=( x-6)'.( 8-4x)+( x-6).(8-4x)'

⇒ f'(x)= 1.( 8 - 4x)+ (x- 6). (-4) = 8- 4x – 4x + 24 = -8x + 32

Chọn A.

Câu 6: Đạo hàm của hàm số y=f(x)= (x+ 2)( x- 3) bằng biểu thức nào?

A. x+ 1        B. 2x- 1        C. 3x+ 2        D. x²- 1

Lời giải:

+ Áp dụng công thức: (u.v)'=u'.v+u.v' ta có:

⇒ f' (x)=(x+2)'.(x-3)+(x+2).(x-3)'

= 1.(x-3) + (x+2). 1 = x- 3+ x+ 2

= 2x - 1

Chọn B.

Câu 7: Tính đạo hàm của hàm số y= (x-6)/(2x+3)?

Lời giải:

Câu 8: Tính đạo hàm của hàm số y= (x²+x+1)/(1-x)?

Lời giải:

Câu 9: Tính đạo hàm của hàm số: y= (x+2)/(x²-1)?

Lời giải:

Câu 10: Tính đạo hàm của hàm số: y=4√x - 4x⁴ + 2x?

Lời giải:

Câu 11: Tính đạo hàm của hàm số: y=(2√x-2).( 2x+1)

Lời giải:

+ Áp dụng công thức ( u.v)'=u'.v+uv' ta có:

y'=( 2√x-2)' ( 2x+1)+( 2√x-2).(2x+1)'

⇒ y'= 2.1/(2√x) (2x+1)+(2√x-2).2

= 2√x+ 1/√x+ 4√x-4= 6√x+ 1/√x-4

Chọn A.

Câu 12: Tính đạo hàm của hàm số y= x³/3+2x²- 1/x?

Lời giải:

Câu 13: Tính đạo hàm của hàm số: y= (x²+2x)/(x²-3x+1)

Lời giải:

Áp dụng công thức đạo hàm của một thương ta có: