Định lý Thalès trong không gian và các bài toán liên quan lớp 11 (bài tập + lời giải)

---

Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Định lý Thalès trong không gian và các bài toán liên quan lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Định lý Thalès trong không gian và các bài toán liên quan.

Định lý Thalès trong không gian và các bài toán liên quan lớp 11 (bài tập + lời giải)

1. Phương pháp giải

- Định lý Thalès trong không gian: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kỳ những đoạn tương ứng tỷ lệ.

- Cách giải các bài toán liên quan: Áp dụng định lí Thalès và định lí Thalès đảo để chứng minh tỷ lệ đoạn thẳng và chứng minh các mặt phẳng song song.

2. Ví dụ minh họa

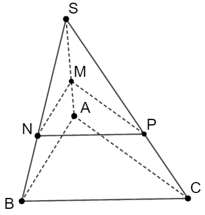
Ví dụ 1.Cho hình chóp S.ABC, mặt phẳng P song song với (ABC) và cắt SA, SB, SC tại M, N, P. Biết SM = 2MA. Tỉ lệ $\frac{SN}{SB}$bằng bao nhiêu?

Hướng dẫn giải:

Vì (P) // (ABC) nên theo định lí Thalès, ta có

$\frac{SM}{SA}=\frac{SN}{SB}=\frac{SP}{SC}=\frac{2}{3}$.

Vậy $\frac{SN}{SB}=\frac{2}{3}$.

3. Bài tập tự luyện

Bài 1. Cho hai đường thẳng d và d’ chéo nhau và các điểm A, B, C trên d, các điểm A’, B’, C’ trên d’ sao cho $\frac{AB}{A\text{'}B\text{'}}=\frac{BC}{B\text{'}C\text{'}}=\frac{AC}{A\text{'}C\text{'}}$. Khi đó các đường thẳng AA’, BB’, CC’

A. Đôi một cắt nhau;

B. Trùng nhau;

C. AA’ song song BB’ và cắt CC’;

D. Song song với nhau.

Bài 2. Cho hình chóp S.ABC. Gọi D, E, F lần lượt là trung điểm của SB, SA, SC. Vị trí tương đối của (DEF) và (ABC) là

A. Song song;

B. Trùng nhau;

C. Cắt nhau;

D. Không xác định được.

Bài 3. Cho hình chóp S.ABC, mặt phẳng (P) song song với (ABC) đi qua trọng tâm G của tam giác SAB và cắt SC tại H. Tỷ lệ $\frac{SH}{SC}$ bằng

A. $\frac{1}{2}$;

B. $\frac{1}{3}$;

C. $\frac{2}{3}$;

D. 1.

Bài 4. Hai hình vuông ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Trên các đường chéo AC vàBF lần lượt lấy hai điểm M vàN sao cho AM = BN. Vị trí tương đối của MN và (CDFE) là

A. Cắt nhau;

B. Song song;

C. MN nằm trên (CDFE);

D. Không đủ điều kiện xác định.

Bài 5. Cho hình bình hành ABCD và một điểm S khôngnằm trên (ABCD, E và F là hai điểm trên SA; SB sao cho: $\frac{SE}{SA}$= $\frac{SF}{SB}$=$\frac{1}{3}$. Vị trí tương đối giữa EF và (ABCD) là

A. EF nằm trên (ABCD);

B. EF cắt (ABCD);

C. EF song song (ABCD);

D. EF và (ABCD) chéo nhau.

Bài 6. Cho tứ diện ABCD. G là trọng tâm của tam giác ABD; M nằm trên AB sao cho AM = 2MB. Vị trí tương đối của MG và (BCD) là

A. MG nằm trên (BCD);

B. MG cắt (BCD);

C. MG song song (BCD);

D. MG và (BCD) chéo nhau.

Bài 7. Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. Trên BC lấy điểm E sao cho EB = 2EC. Vị trí tương đối của EG và (ACD) là

A. EG nằm trên (ACD);

B. EG song song (ACD);

C. EG cắt (ACD);

D. EG và (ACD) chéo nhau.

Bài 8. Cho tứ diện ABCD. Gọi E, F là trọng tâm các tam giác ACD và ABD. Vị trí tương đối của EF và ABC là

A. EF song song (ABC);

B. EF nằm trên (ABC);

C. EF vuông góc (ABC);

D. EF cắt (ABC).

Bài 9. Cho hình chóp S.ABC; gọi G, H là trọng tâm tam giác SAC và SBC. Gọi M là trung điểm của BC. Đường thẳng song song với (ABC) là

A. GM;

B. HM;

C. GH;

D. GS.

Bài 10. Cho tứ diện ABCD; lấy điểm M trên cạnh AB sao cho: $\frac{AM}{AB}=\frac{1}{4}$. Trên cạnh AC lấy điểm N sao cho MN // (BCD). Tỉ số $\frac{AN}{NC}$là

A. $\frac{1}{2}$;

B. $\frac{1}{3}$;

C. 2;

D. 3.