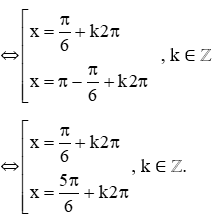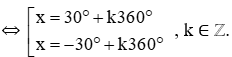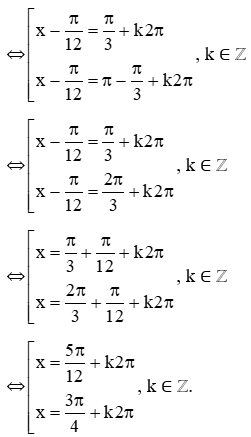Giải phương trình lượng giác bằng cách vận dụng phương trình lượng giác cơ bản lớp 11 (bài tập + lời giải)

---

Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Giải phương trình lượng giác bằng cách vận dụng phương trình lượng giác cơ bản lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Giải phương trình lượng giác bằng cách vận dụng phương trình lượng giác cơ bản.

Giải phương trình lượng giác bằng cách vận dụng phương trình lượng giác cơ bản lớp 11 (bài tập + lời giải)

1. Phương pháp giải

* Phương pháp giải: Để Giải phương trình lượng giác bằng cách vận dụng phương trình lượng giác cơ bản, ta cần nhận dạng (biến đổi) phương trình đã cho về đúng loại phương trình cơ bản, từ đó chọn và ráp công thức nghiệm tương ứng.

* Đổi đơn vị: π = 180°.

* Các phương trình lượng giác cơ bản:

* Phương trình sin x = a(1)

+ TH1: |a| > 1: phương trình (1) vô nghiệm.

+ TH2: |a| ≤ 1: gọi α là một góc thỏa mãn sin α = a.

Khi đó, phương trình (1) có các nghiệm là:

x = α + k2π, k ∈ ℤ hoặc x = π – α + k2π, k ∈ ℤ.

Chú ý:

√ Nếu số đo góc α được cho bằng đơn vị độ thì ta có các nghiệm là

x = α° + k360°, k ∈ ℤ hoặc x = 180° – α° + k360°, k ∈ ℤ.

√ Một số trường hợp đặc biệt:

 sin x = 1 ⇔ $x=\frac{\pi }{2}+k2\pi$, k ∈ ℤ hoặc x = 90° + k360°, k ∈ ℤ.

sin x = –1 ⇔ $x=-\frac{\pi }{2}+k2\pi$, k ∈ ℤ hoặc x = –90° + k360°, k ∈ ℤ.

 sin x = 0 ⇔ x = kπ, k ∈ ℤ hoặc x = k180°, k ∈ ℤ.

* Phương trình cos x = a(2)

+ TH1: |a| > 1: phương trình (2) vô nghiệm.

+ TH2: |a| ≤ 1: gọi α là một góc thỏa mãn cos α = a.

Khi đó, phương trình (2) có các nghiệm là:

x = α + k2π, k ∈ ℤ hoặc x = – α + k2π, k ∈ ℤ.

Chú ý:

√ Nếu số đo góc α được cho bằng đơn vị độ thì ta có các nghiệm là

x = α° + k360°, k ∈ ℤ hoặc x = –α° + k360°, k ∈ ℤ.

√ Một số trường hợp đặc biệt:

 cos x = 1 ⇔ x = k2π, k ∈ ℤ hoặc x = k360°, k ∈ ℤ.

 cos x = –1 ⇔ x = π + k2π, k ∈ ℤ hoặc x = 180° + k360°, k ∈ ℤ.

 cos x = 0 ⇔ $x=\frac{\pi }{2}+k\pi$, k ∈ ℤ hoặc x = 90° + k360°, k ∈ ℤ.

* Phương trình tan x = a (3)

Điều kiện xác định: $x\ne \frac{\pi }{2}+k\pi$, k ∈ ℤ hoặc $x\ne 90°+k180°,k\in \mathbb{Z}$.

Khi đó, phương trình (3) có nghiệm là x = α + kπ, k ∈ ℤ.

Chú ý: Nếu số đo góc α được cho bằng đơn vị độ thì ta có nghiệm là

x = α° + k180°, k ∈ ℤ.

* Phương trình cot x = a (4)

Chú ý: Nếu số đo góc α được cho bằng đơn vị độ thì ta có nghiệm là

x = α° + k180°, k ∈ ℤ.

2. Ví dụ minh họa

Ví dụ 1. Giải các phương trình lượng giác sau:

a) cos x = 3;

b) sin x = $\frac{1}{2}$;

c) cos x $=\frac{\sqrt{3}}{2}$;

d) cos $\left(x-\frac{5\pi }{12}\right)$= 1;

e) sin$\left(x-\frac{\pi }{12}\right)=\frac{\sqrt{3}}{2}$.

Hướng dẫn giải:

a) cos x = 3 (1)

Vì –1 ≤ cos x ≤ 1 với mọi số thực x nên phương trình (1) vô nghiệm.

b) sin x = $\frac{1}{2}$

⇔ sin x = sin$\frac{\pi }{6}$

c) cos x $=\frac{\sqrt{3}}{2}$

⇔ cos x = cos 30°

d) cos $\left(x-\frac{5\pi }{12}\right)$= 1

⇔$x-\frac{5\pi }{12}$ = k2π , k ∈ ℤ

⇔x = $\frac{5\pi }{12}$+ k2π, k ∈ ℤ.

e) sin$\left(x-\frac{\pi }{12}\right)=\frac{\sqrt{3}}{2}$

⇔ sin$\left(x-\frac{\pi }{12}\right)=\sin \frac{\pi }{3}$

Ví dụ 2. Giải các phương trình lượng giác sau:

a) tan $\left(x+\frac{\pi }{2}\right)$= $\sqrt{3}$;

b) cot $\left(x+\frac{3\pi }{4}\right)$= $\sqrt{3}$.

Hướng dẫn giải:

a) tan$\left(x+\frac{\pi }{2}\right)$= $\sqrt{3}$

⇔ $\tan \left(x+\frac{\pi }{2}\right)=\tan \frac{\pi }{3}$

⇔ $x+\frac{\pi }{2}=\frac{\pi }{3}+k\pi$, k ∈ ℤ

⇔$x=\frac{-\pi }{6}+k\pi$, k ∈ ℤ.

b) cot $\left(x+\frac{3\pi }{4}\right)$= $\sqrt{3}$

⇔ cot $\left(x+\frac{3\pi }{4}\right)$ = $\cot \frac{\pi }{6}$

⇔ $x+\frac{3\pi }{4}=\frac{\pi }{6}+k\pi$, k ∈ ℤ

⇔ $x=\frac{-7\pi }{12}+k\pi$, k ∈ ℤ.

3. Bài tập tự luyện 

Bài 1. Phương trình nào sau đây vô nghiệm?

A. sin x = 5;

B. cos x = $\frac{1}{3}$;

C. tan x = 10;

D. cot x = 4.

Bài 2. Nghiệm của phương trình sin x = 1 là

A. $x=\frac{\pi }{2}+k2\pi$, k ∈ ℤ;

B. x = k2π, k ∈ ℤ;

C. x = kπ, k ∈ ℤ;

D. $x=\frac{\pi }{3}+k2\pi$, k ∈ ℤ.

Bài 3. Đáp án nào sau đây không phải là một nghiệm của phương trình cos x = 0?

A. 90°;

B. – 90°;

C. 30°;

D. 270°.

Bài 4. Đáp án nào sau đây không phải là một nghiệm của phương trình sin x = –1 ?

A. $-\frac{\pi }{2}$;

B. $\frac{-5\pi }{2}$;

C. $\frac{3\pi }{2}$;

D. $\frac{5\pi }{2}$.

Bài 5. Họ nghiệm của phương trình tan x =$\sqrt{3}$ là

A. x = 45° + k360°, k ∈ ℤ;

B. x = 45° + k180°, k ∈ ℤ;

C. x = 60° + k360°, k ∈ ℤ;

D. x = 60° + k180°, k ∈ ℤ.

Bài 6. Họ nghiệm của phương trình cot x = 2 là

A. x = 2 + k2π, k ∈ ℤ;

B. x = arccot 2 + k2π, k ∈ ℤ;

C. x = 2 + kπ, k ∈ ℤ;

D. x = arccot 2 + kπ, k ∈ ℤ.

Bài 7. Đáp án nào sau đây không phải là một nghiệm của phương trình $\tan \left(x+\frac{\pi }{3}\right)=\sqrt{3}$?

A. x = 0;

B. x = $\frac{4\pi }{3}$;

C. x = π;

D. x = 2π.

Bài 8. Nghiệm của phương trình $\tan \left(x+\frac{\pi }{3}\right)=\sqrt{3}$là

A. x = kπ, k ∈ ℤ ;

B. x = $\frac{4\pi }{3}$+ kπ, k ∈ ℤ;

C. x = $\frac{\pi }{3}$+ kπ, k ∈ ℤ;

D. x = $\frac{\pi }{2}$+ kπ, k ∈ ℤ.

Bài 9. Nghiệm của phương trình $\cos \left(x-\frac{\pi }{3}\right)=\frac{1}{2}$là

A. x = kπ, k ∈ ℤ;

B. x = $\frac{4\pi }{3}$+ k2π, k ∈ ℤ;

C. x =$\frac{\pi }{3}$+ k2π và x = –$\frac{\pi }{3}$+ k2π, k ∈ ℤ;

D. x = $\frac{2\pi }{3}$+ k2πvà x = k2π, k ∈ ℤ.

Bài 10. Nghiệm của phương trình $\sin \left(2x+\frac{2\pi }{3}\right)=1$là

A. x = $\frac{-\pi }{12}$+ kπ, k ∈ ℤ;

B. x = $\frac{\pi }{2}$+ kπ, k ∈ ℤ;

C. x = $\frac{\pi }{3}$+ k2π và x = –$\frac{\pi }{3}$+ k2π, k ∈ ℤ;

D. x = $\frac{2\pi }{3}$+ k2πvà x = $\frac{\pi }{2}$+ k2π, k ∈ ℤ.