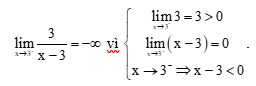Giới hạn vô cực của hàm số tại một điểm lớp 11 (bài tập + lời giải)

---

Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Giới hạn vô cực của hàm số tại một điểm lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Giới hạn vô cực của hàm số tại một điểm.

Giới hạn vô cực của hàm số tại một điểm lớp 11 (bài tập + lời giải)

1. Phương pháp giải

- Ta có thể áp dụng các quy tắc về giới hạn tới vô cực         

$\underset{x\to x_0}{\lim }f\left(x\right)=L$		Dấu của g(x)	$\underset{x\to x_0}{\lim }\frac{f\left(x\right)}{g\left(x\right)}$
L	±∞	Tùy ý	0
L > 0	0	+	+∞
	0	−	−∞
L < 0	0	+	−∞
	0	−	+∞

$\underset{x\to x_0}{\lim }f\left(x\right)=L$	$\underset{x\to x_0}{\lim }g\left(x\right)$	$\underset{x\to x_0}{\lim }f\left(x\right)g\left(x\right)$
L > 0	+∞	+∞
	−∞	−∞
L < 0	+∞	−∞
	−∞	+∞

2. Ví dụ minh họa:

Ví dụ 1.

Tính giới hạn $\underset{x\to 3^{-}}{\lim }\frac{3}{x-3}$

Hướng dẫn giải:

3. Bài tập tự luyện

Bài 1. Giới hạn $\underset{x\to 4^{-}}{\lim }\frac{7}{x-4}$ bằng

A. 0;

B. −∞;

C. +∞;

D. 1.

Bài 2. Giới hạn $\underset{x\to 4}{\lim }\frac{3}{\sqrt{x-4}}$ bằng

A. 0;

B. −∞;

C. +∞;

D. 1.

Bài 3. Giới hạn $\underset{x\to 3^{-}}{\lim }\frac{x-2}{x-3}$ bằng

A. 0;

B. −∞;

C. +∞;

D. 1.

Bài 4. Tính giới hạn $\underset{x\to 3^{-}}{\lim }\frac{2x-1}{{\left(x-3\right)}^2}$, ta thu được kết quả nào sau đây?

A. 0;

B. −∞;

C. +∞;

D. 1.

Bài 5. Giới hạn $\underset{x\to -1}{\lim }\frac{x^2+x}{{\left(x+1\right)}^3}$ bằng

A. 0;

B. −∞;

C. +∞;

D. 1.

Bài 6. Tính giới hạn $\underset{x\to 0}{\lim }\left(\frac{1}{x}-\frac{1}{x^2}\right)$, ta thu được kết quả nào sau đây?

A. 0;

B. −∞;

C. +∞;

D. 1.

Bài 7. Giới hạn 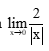 bằng

A. 0;

B. −∞;

C. +∞;

D. 1.

Bài 8. Giới hạn 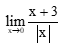bằng

A. 0;

B. −∞;

C. +∞;

D. 1.

Bài 9. Tính giới hạn 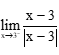, ta thu được kết quả nào sau đây?

A. 0;

B. −∞;

C. +∞;

D. −1.

Bài 10. Giới hạn $\underset{x\to 3}{\lim }\frac{x^2-5x+6}{x^2-6x+9}$ bằng

A. 0;

B. −∞;

C. +∞;

D. 1.