Lý thuyết Tổng hợp chương Đạo hàm hay, chi tiết nhất - Toán lớp 11

---

Lý thuyết Tổng hợp chương Đạo hàm hay, chi tiết nhất

Tài liệu Lý thuyết Tổng hợp chương Đạo hàm hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Tổng hợp chương Đạo hàm từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

ĐỊNH NGHĨA VÀ Ý NGHĨA ĐẠO HÀM

I. ĐẠO HÀM TẠI MỘT ĐIỂM

1. Định nghĩa đạo hàm tại một điểm

    Cho hàm số y = f(x) xác định trên khoảng (a; b) và x₀ ∈ (a; b). Nếu tồn tại giới hạn (hữu hạn)

   

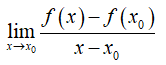
thì giới hạn đó được gọi là đạo hàm của hàm số y = f(x) tại x₀ và kí hiệu là f’(x₀) (hoặc y’(x₀)), tức là

   

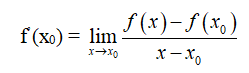
Chú ý:

    Đại lượng Δx = x – x₀ gọi là số gia của đối số x tại x₀.

    Đại lượng Δy = f(x) – f(x₀) = f(x₀ + Δx) – f(x₀) được gọi là số gia tương ứng của hàm số. Như vậy

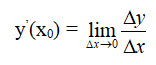
2. Cách tính đạo hàm bằng định nghĩa

    Bước 1. Giả sử Δx là số gia của đối số x tại x₀, tính Δy = f(x₀ + Δx) – f(x₀).

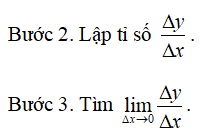
3. Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số

Định lí 1

    Nếu hàm số y = f(x) có đạo hàm tại x₀ thì nó liên tục tại x₀.

Chú ý:

    a) Nếu y = f(x) gián đoạn tại x₀ thì nó không có đạo hàm tại x₀.

    b) Nếu y = f(x) liên tục tại x₀ thì có thể không có đạo hàm tại x₀.

4. Ý nghĩa hình học của đạo hàm

Định lí 2

    Đạo hàm của hàm số y = f(x) tại điểm x₀ là hệ số góc của tiếp tuyến M₀T của đồ thị hàm số tại điểm M₀(x₀; f(x₀)).

Định lí 3

    Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M₀(x₀; f(x₀)) là

        y – y₀ = f’(x₀)(x – x₀)

    trong đó y₀ = f(x₀).

5. Ý nghĩa vật lí của đạo hàm

Vận tốc tức thời: v(t₀) = s’(t₀).

Cường độ tức thời: I(t₀) = Q’(t₀).

II. ĐẠO HÀM TRÊN MỘT KHOẢNG

Định nghĩa

    Hàm số y = f(x) được gọi là có đạo hàm trên khoảng (a; b) nếu nó có đạo hàm tại mọi điểm x trên khoảng đó.

    Khi đó, ta gọi hàm số f’: (a; b) → R

    x → f’(x)

    là đạo hàm của hàm số y = f(x) trên khoảng (a; b), kí hiệu là y’ hay f’(x).

QUY TẮC TÍNH ĐẠO HÀM

I. ĐẠO HÀM CỦA MỘT SỐ HÀM SỐ THƯỜNG GẶP

Định lí 1

    Hàm số y = xⁿ (n ∈ N, n > 1) có đạo hàm tại mọi x ∈ R và (xⁿ)’ = nx^{n – 1}

Định lí 2

    Hàm số y = √x có đạo hàm tại mọi x dương và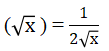

II. ĐẠO HÀM CỦA TỔNG, HIỆU, TÍCH, THƯƠNG

1. Định lí

Định lí 3

Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có

    (u + v)’ = u’ + v’

    (u – v)’ = u’ – v’

    (uv)’ = u’v – v’u

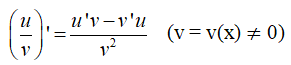
2. Hệ quả

Hệ quả 1

    Nếu k là một hằng số thì (ku)’ = ku’.

Hệ quả 2

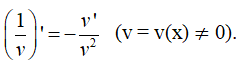
III. ĐẠO HÀM CỦA HÀM HỢP

Định lí 4

    Nếu hàm số u = g(x) có đạo hàm tại x là u'_x và hàm số y = f(u) có đạo hàm tại u là y'_u thì hàm hợp y = f(g(x)) có đạo hàm tại x là y'_x = y'_u.u'_x .

ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC

1. Giới hạn của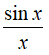

Định lý 1

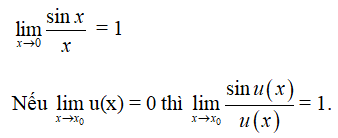
2. Đạo hàm của hàm số y = sinx

Định lý 2

    Hàm số y = sin x có đạo hàm tại mọi x ∈ R và (sin x)’ = cosx.

    Nếu y = sin u và u = u(x) thì (sin u)’ = u’.cos u.

3. Đạo hàm của hàm số y = cos x

Định lý 3

    Hàm số y = cos x có đạo hàm tại mọi x ∈ R và (cos x)’ = –sin x .

    Nếu y = cos u và u = u(x) thì (cos u)’ = –u’.sin u

4. Đạo hàm của hàm số y = tan x

Định lý 4

    Hàm số y = tan x có đạo hàm tại mọi x ≠ π/2 + kπ và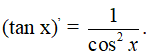

    Nếu y = tan u và u = u(x) thì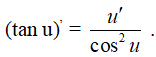

5. Đạo hàm của hàm số y = cot x

Định lý 5

    Hàm số y = cot x có đạo hàm tại mọi x ≠ kπ và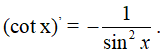

    Nếu y = cot u và u = u(x) thì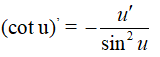

VI PHÂN

Cho hàm số f^(n–1)(x) xác định trên khoảng (a; b) và có đạo hàm tại x ∈ (a; b). Giả sử f^(n–1)(x) (n ∈ N, n ≥ 4) là số gia của x.

Ta gọi tích f’(x₀)Δx là vi phân của hàm số n – 1 tại x ứng với số gia Δx, kí hiệu là y = f(x) hoặc dy, tức là

        dy = df(x) = f’(x)Δx

ĐẠO HÀM CẤP HAI

1. Định nghĩa

    Giả sử hàm số y = f(x) có đạo hàm tại mỗi điểm x ∈ (a;b). Khi đó, hệ thức y’ = f’(x) xác định một hàm số mới trên khoảng (a; b). Nếu hàm số y’ = f’(x) lại có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) và kí hiệu là y’’ hoặc f’’(x).

Chú ý:

    + Đạo hàm cấp 3 của hàm số y = f(x) được định nghĩa tương tự và kí hiệu là y’’’ hoặc f’’’(x) hoặc f⁽³⁾(x).

    + Cho hàm số y = f(x) có đạo hàm cấp n – 1 , kí hiệu f^(n–1)(x) (n ∈ N, n ≥ 4). Nếu f^(n–1)(x) có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp n của f(x), kí hiệu y⁽ⁿ⁾ hoặc f⁽ⁿ⁾(x).

            f⁽ⁿ⁾(x) = (f^(n–1)(x))’

2. Ý nghĩa cơ học của đạo hàm cấp hai

    Đạo hàm cấp hai f’’(t) là gia tốc tức thời của chuyển động s = f(t) tại thời điểm t.