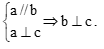Nhận biết và chứng minh đường thẳng vuông góc lớp 11 (bài tập + lời giải)

---

Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Nhận biết và chứng minh đường thẳng vuông góc lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Nhận biết và chứng minh đường thẳng vuông góc .

Nhận biết và chứng minh đường thẳng vuông góc lớp 11 (bài tập + lời giải)

1. Phương pháp giải

- Định nghĩa: Hai đường thẳng a, b được gọi là vuông góc với nhau, kí hiệu a ⊥ b, nếu góc giữa chúng bằng 90°.

- Để chứng minh hai đường thẳng vuông góc trong không gian:

+ Cách 1. Sử dụng định nghĩa: Tính số đo góc của hai đường thẳng đó và chứng minh nó bằng 90°.

+ Cách 2. Áp dụng tính chất từ vuông góc đến song song:

+ Cách 3. Sử dụng tích vô hướng: Tìm hai vectơ chỉ phương ,  của hai đường thẳng d₁, d₂. Khi đó $d_1\perp d_2\iff \overrightarrow{u_1}.\overrightarrow{u_2}=0$ .

+ Cách 4. Sử dụng các tính chất trong hình học phẳng: đường cao, đường trung trực, định lí Pythagore, …

2. Ví dụ minh họa

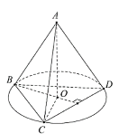
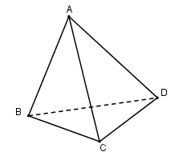
Ví dụ 1. Cho tứ diện ABCD đều cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh AO vuông góc với CD.

Lời giải

Do tứ diện ABCD đều nên các tam giác ACD, BCD là các tam giác đều.

Vì O là tâm đường tròn ngoại tiếp tam giác BCD nên O vừa là trọng tâm, vừa là trực tâm, vừa là giao 3 đường phân giác của tam giác BCD.

Khi đó ta suy ra được CA = CD = a, CO =$\frac{a\sqrt{3}}{3}$ , $\widehat{ACD}=60°,\widehat{OCD}=30°$ .

Ta có: $\overrightarrow{AO}.\overrightarrow{CD}=\left(\overrightarrow{CO}-\overrightarrow{CA}\right).\overrightarrow{CD}$

$=\overrightarrow{CO}.\overrightarrow{CD}-\overrightarrow{CA}.\overrightarrow{CD}=CO.CD.\cos 30°-CA.CD.\cos 60°$

$=\frac{a\sqrt{3}}{3}.a.\frac{\sqrt{3}}{2}-a.a.\frac{1}{2}=\frac{a^2}{2}-\frac{a^2}{2}=0$.

Suy ra AO vuông góc với CD.

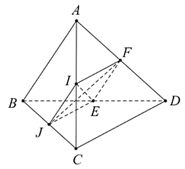
Ví dụ 2. Cho tứ diện ABCD có AB = CD. Gọi I, J, E, F lần lượt là trung điểm của AC, BC, BD, AD. Chứng minh IE và JF vuông góc với nhau.

Hướng dẫn giải

Tứ giác IJEF là hình bình hành

Mặt khác: 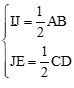 mà AB = CD nên IJ = JE

Do đó, IJEF là hình thoi.

Vậy IE và JF vuông góc với nhau.

3. Bài tập tự luyện

Câu 1. Cho hai tam giác cân ABC và DBC có chung cạnh đáy BC nằm trong hai mặt phẳng khác nhau. Khẳng định nào sau đây là đúng nhất?

A. AD vuông góc với BC;

B. AD song song với BC;

C. AD cắt BC tại một điểm;

D. Không có khẳng định nào đúng.

Câu 2. Cho hình chóp S.ABC có SA = SB = SC và $\widehat{ASB}=\widehat{BSC}=\widehat{CSA}$ . Khẳng định nào sau đây là đúng?

A. SA vuông góc với AB;

B. SB vuông góc với SC;

C. SA vuông góc với BC;

D. SA vuông góc với AB.

Câu 3. Cho hình lập phương ABCD.A₁B₁C₁D₁. Chọn khẳng định đúng?

A. Góc giữa AC và BD₁ bằng $90°$ ;

B. Góc giữa B₁D₁ và AA₁ bằng $90°$ ;

C. Góc giữa AD và B₁C bằng $90°$ ;

D. Góc giữa B₁A₁ và A₁C₁ bằng $90°$ .

Câu 4. Mệnh đề nào sau đây là đúng?

A. Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song với nhau;

B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại;

C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau;

D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.

Câu 5. Cho hai tam giác cân ABC và DBC có chung cạnh đáy BC nằm trong hai mặt phẳng khác nhau. Gọi M, N là các điểm lần lượt thuộc các đường thẳng AB và DB sao cho $\overrightarrow{MA}=k\overrightarrow{MB}$  , $\overrightarrow{ND}=k\overrightarrow{NB}$ . Hai đường thẳng MN và BC có quan hệ:

A. vuông góc;

B. song song;

C. trùng nhau;

D. cắt nhau.

Câu 6. Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AC, BC, BD, DA. Khẳng định nào sau đây là đúng nhất?

A. MNPQ là hình vuông;

B. MNPQ là hình bình hành;

C. MNPQ là hình chữ nhật;

D. MNPQ là hình thoi.

Câu 7. Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (MN, SC) bằng:

A. $45°$ ;                

B. $30°$ ;                

C. $90°$ ;                

D. $60°$ .

Câu 8. Cho tứ diện ABCD có AB = AC = AD và $\widehat{BAC}=\widehat{BAD}=60°$ , $\widehat{CAD}=90°$ . Gọi I, J lần lượt là trung điểm của AB và CD. Khẳng định nào sau đây là đúng?

A. AC và IJ vuông góc với nhau;

B. AB là IJ vuông góc với nhau;

C. BD và IJ vuông góc với nhau;

D. AD và IJ vuông góc với nhau.

Câu 9. Trong không gian cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây đúng ?

A. Nếu a và b cùng vuông góc với c thì a // b;

B. Nếu a // b và c ⊥ a thì c ⊥ b;

C. Nếu góc giữa a và c bằng góc giữa b và c thì a // b

D. Nếu a và b cùng nằm trong mặt phẳng song song với c thì góc giữa a và c bằng góc giữa b và c.

Câu 10. Cho bài toán sau:

Cho tứ diện ABCD. Chứng minh rằng nếu: $\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AC}.\overrightarrow{AD}=\overrightarrow{AD}.\overrightarrow{AB}$  thì AB vuông góc với CD, AC vuông góc với BD, AD vuông góc với BC. Điều ngược lại đúng không?

Sau đây là lời giải

Bước 1:

$\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AC}.\overrightarrow{AD}\iff \overrightarrow{AC}\left(\overrightarrow{AB}-\overrightarrow{AD}\right)=0\iff \overrightarrow{AC}.\overrightarrow{DB}=0$

Do đó, AC vuông góc với BD.

Bước 2: Chứng minh tương tự, từ $\overrightarrow{AC}.\overrightarrow{AD}=\overrightarrow{AD}.\overrightarrow{AB}$  ta được AD vuông góc với BC và $\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AD}.\overrightarrow{AB}$  ta được AB vuông góc với CD.

Bước 3: Ngược lại đúng, vì quá trình chứng minh ở bước 1, bước 2 là quá trình biến đổi tương đương.

Hướng giải trên đúng hay sai? Nếu sai thì sai ở đâu?

A. Sai ở bước 3;

B. Đúng;

C. Sai ở bước 2;

D. Sai ở bước 1.