Phương pháp giải phương trình lượng giác cơ bản

---

Phương pháp giải phương trình lượng giác cơ bản

Với Phương pháp giải phương trình lượng giác cơ bản Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải phương trình lượng giác cơ bản từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

1. Lý thuyết

a) Phương trình sin x = m

Trường hợp 1: |m| > 1. Phương trình vô nghiệm.

Trường hợp 2: |m| ≤ 1 . Phương trình có nghiệm.

- Nếu m biểu diễn được dưới dạng sin của những góc đặc biệt thì:

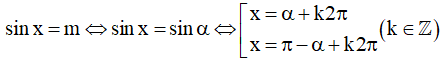
- Nếu m không biểu diễn được dưới dạng sin của những góc đặc biệt thì:

- Các trường hợp đặc biệt:

sin x = 0 ⇔ x = kπ (k ∈ Z)

sin x = 1 ⇔ x = 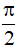+ k2π (k ∈ Z)

sin x = -1 ⇔ x = -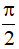 + k2π (k ∈ Z)

b) Phương trình cos x = m

Trường hợp 1: |m| > 1. Phương trình vô nghiệm.

Trường hợp 2: |m| ≤ 1 . Phương trình có nghiệm.

- Nếu m biểu diễn được dưới dạng cos của những góc đặc biệt thì:

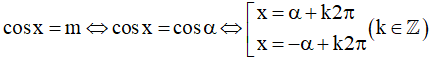
- Nếu m không biểu diễn được dưới dạng cos của những góc đặc biệt thì:

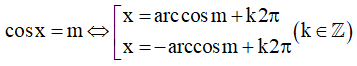
- Các trường hợp đặc biệt:

cos x = 0 ⇔ x = 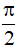+ k2π (k ∈ Z)

cos x = 1 ⇔ x = k2π (k ∈ Z)

cos x = -1 ⇔ x = π + kπ (k ∈ Z)

c) Phương trình: tan x = m. Điều kiện: x ≠ 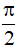+ k2π (k ∈ Z)

- Nếu m biểu diễn được dưới dạng tan của những góc đặc biệt thì:

tan x = m ⇔ tan x = tan α ⇔ x = α + kπ (k ∈ Z)

- Nếu m không biểu diễn được dưới dạng tan của những góc đặc biệt thì:

tan x = m ⇔ x = αrctan m + kπ (k ∈ Z)

d) Phương trình: cot x = m. Điều kiện: x ≠ kπ(k ∈ Z)

- Nếu m biểu diễn được dưới dạng cot của những góc đặc biệt thì:

cot x = m ⇔ cot x = cot α ⇔ x = α + kπ (k ∈ Z)

- Nếu m không biểu diễn được dưới dạng cot của những góc đặc biệt thì:

cot x = m ⇔ x = αrccot m + kπ (k ∈ Z)

e) Chú ý:

Nếu gặp bài toán yêu cầu tìm số đo độ của góc lượng giác sao cho sin (cos, tan, cot) của chúng bằng m.

Ví dụ: 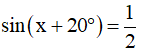ta có thể áp dụng các công thức nghiệm nêu trên, lưu ý sử dụng kí hiệu số đo độ trong công thức nghiệm.

Đối với ví dụ trên ta viết: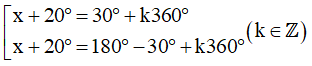

chứ không viết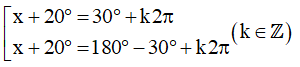

2. Phương pháp giải:

Sử dụng công thức nghiệm cơ bản của phương trình lượng giác.

Mở rộng công thức nghiệm, với u(x) và v(x) là hai biểu thức của x.

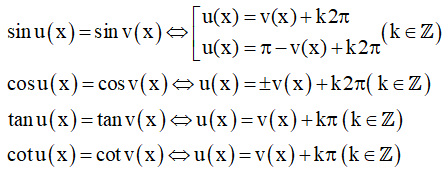
3. Ví dụ minh họa

Ví dụ 1: Giải các phương trình sau:

a)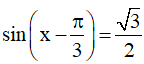

b) 3cos(x+1) = 1

c) tan(3x + 15⁰) = √3

d)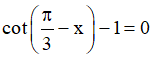

Lời giải

a)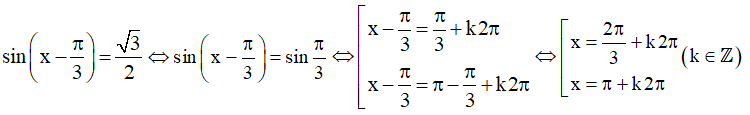

Vậy họ nghiệm của phương trình là: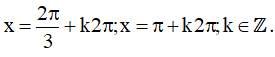

b) 3cos(x+1) = 1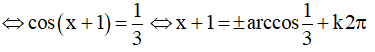

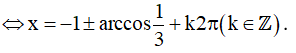
Vậy họ nghiệm của phương trình là: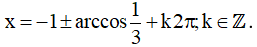

c) Điều kiện xác định: cos(3x + 15⁰) ≠ 0

⇔ 3x + 15⁰ ≠ 90⁰ + k180

⇔ 3x ≠ 75⁰ + k180

⇔ x ≠ 25⁰ + k60⁰ (k ∈ Z)

Ta có: tan(3x + 15⁰) = √3

⇔ tan(3x + 15⁰) = tan60⁰

⇔ 3x + 15⁰ = 60⁰ + k180

⇔ x = 15⁰ + k60⁰ (k ∈ Z) (Thỏa mãn)

Vậy họ nghiệm của phương trình là: x = 15⁰ + k60⁰ (k ∈ Z)

d) Điều kiện xác định: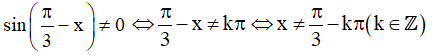

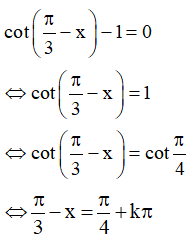
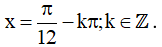⇔ (Thỏa mãn)

Vậy họ nghiệm của phương trình là: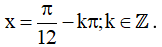

Ví dụ 2: Giải các phương trình sau:

a)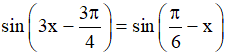

b) cos5x – sinx = 0

c)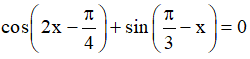

d)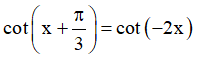

Lời giải

a)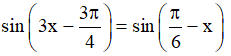

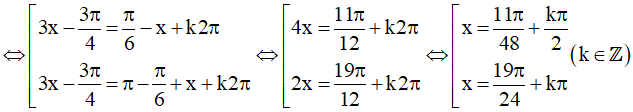
Vậy họ nghiệm của phương trình là: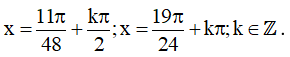

b) cos5x – sinx = 0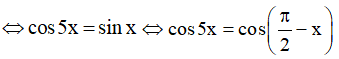

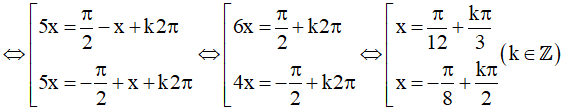
Vậy họ nghiệm của phương trình là: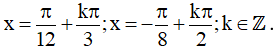

c)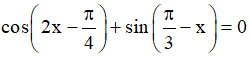

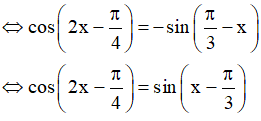
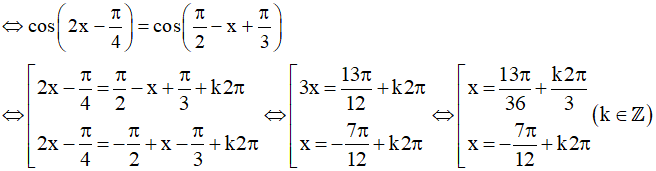
Vậy họ nghiệm của phương trình là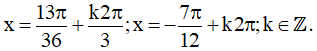

d) Điều kiện xác định: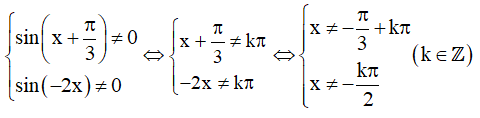

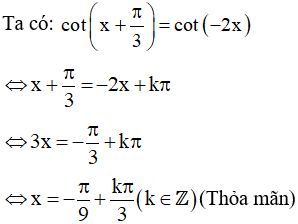
Vậy họ nghiệm của phương trình là: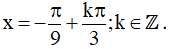

Ví dụ 3: Giải các phương trình sau:

a) (1 + 2cosx)(3 – cosx) = 0

b) (cotx + 1)sin3x = 0

c)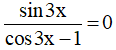

d) tanx.tan2x = 1

Lời giải

a) (1 + 2cosx)(3 – cosx) = 0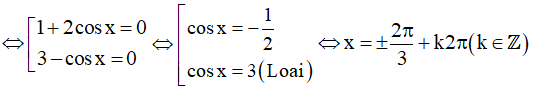

Vậy họ nghiệm của phương trình là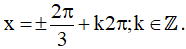

b) Điều kiện xác định: sinx ≠ 0 ⇔ x ≠ kπ(k ∈ Z)

Ta có: (cotx + 1)sin3x = 0

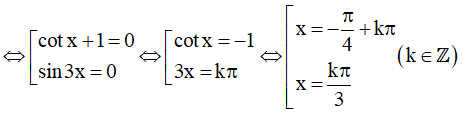
Kết hợp với điều kiện xác định ta được họ nghiệm của phương trình là: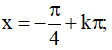

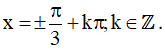
c) Điều kiện xác định: cos3x - 1 ≠ 0 ⇔ cos3x ≠ 1 ⇔ 3x ≠ k2π ⇔ .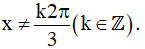

Ta có: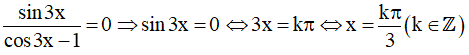

Kết hợp với điều kiện xác định ta được họ nghiệm của phương trình là: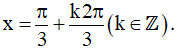

d) Điều kiện xác định: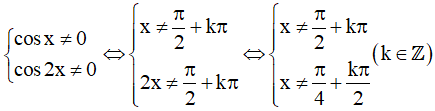

tanx.tan2x = 1 (*)

Trường hợp 1: tanx = 0. Thay vào (*) (vô lí).

Trường hợp 2: tanx ≠ 0 ⇔ x ≠ kπ (k ∈ Z)

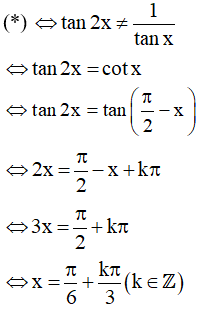
Kết hợp với điều kiện xác định ta được họ nghiệm của phương trình là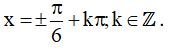

4. Bài tập tự luyện

Câu 1. Họ nghiệm của phương trình 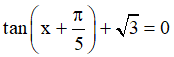là

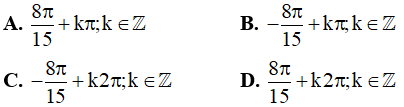
Câu 2. Số nghiệm của phương trình: 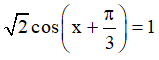với 0 ≤ x ≤ 2π là :

A. 0 B. 2 C. 1 D. 3

Câu 3. Các nghiệm phương trình 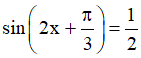là:

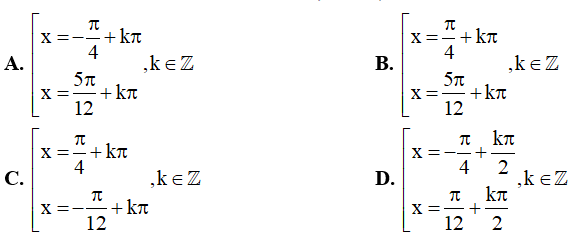
Câu 4. Các nghiệm của phương trình 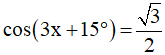là:

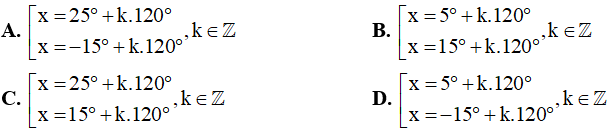
Câu 5. Nghiệm của phương trình 2sinx.cosx = 1 là:

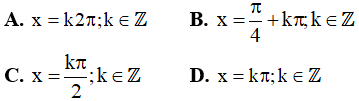
Câu 6. Phương trình 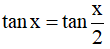có họ nghiệm là:

A. x = k2π,k ∈ Z B. x = kπ,k ∈ Z C. x = π + k2π,k ∈ Z D. x = 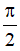+ kπ,k ∈ Z

Câu 7. Nghiệm của phương trình sin3x = cosx là:

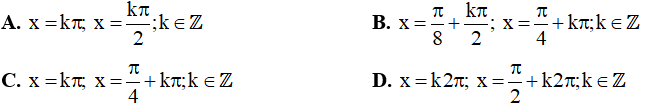
Câu 8. Nghiệm âm lớn nhất và nghiệm dương nhỏ của phương trình sin 4x + cos5x = 0 theo thứ tự là:

Câu 9. Giải phương trình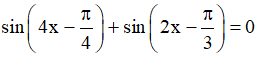

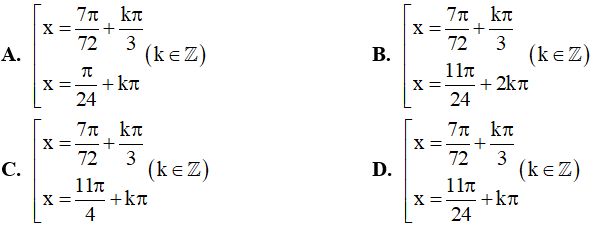
Câu 10. Nghiệm của phương trình sinx(2cosx - √3) = 0 là:

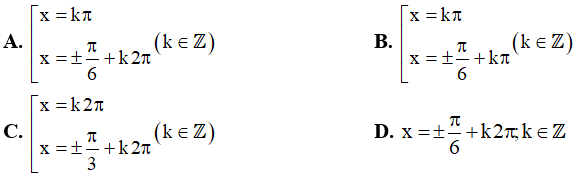
Câu 11. Nghiệm của phương trình tanx = cotx

Câu 12. Nghiệm của phương trình tan3x.cot2x = 1 là

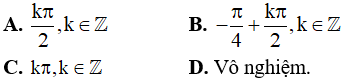
Câu 13. Phương trình (sinx + 1)(sinx - √2) = 0 có các nghiệm là:

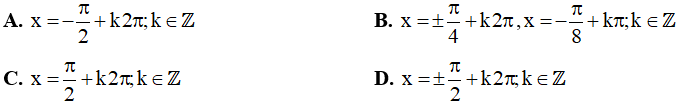
Câu 14. Giải phương trình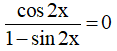

Câu 15. Tìm tổng các nghiệm của phương trình 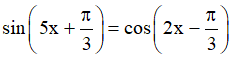trên [0,π]

Bảng đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
B	B	C	D	B	A	B	C	D	A	A	D	A	D	D