Phương pháp Tìm tập xác định, tập giá trị của hàm số lượng giác

---

Phương pháp Tìm tập xác định, tập giá trị của hàm số lượng giác

Với Phương pháp Tìm tập xác định, tập giá trị của hàm số lượng giác Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm tập xác định, tập giá trị của hàm số lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

1. Lý thuyết

a. Hàm số y = sinx

- Tập xác định: D = R

- Tập giá trị: [-1;1]

b. Hàm số y = cosx

- Tập xác định: D = R

- Tập giá trị: [-1;1]

c. Hàm số y = tanx

- Tập xác định: D = R \ { 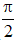+ kπ, k ∈ Z}

- Tập giá trị:R

d. Hàm số y = cotx

- Tập xác định: D = R \ { kπ, k ∈ Z}

- Tập giá trị: R

2. Các dạng bài tập

Dạng 1. Tìm tập xác định của hàm số lượng giác

- Phương pháp giải:

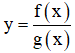xác định khi g(x) ≠ 0

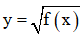xác định khi f(x) ≥ 0

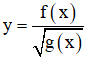xác định khi g(x) > 0

y = tan[u(x)] xác định khi u(x) ≠ 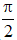+ kπ, k ∈ Z

y = cot[u(x)] xác định khi u(x) ≠ kπ, k ∈ Z

sin x ≠ 0 khi x ≠ kπ (k ∈ Z)

cos x ≠ 0 khi x ≠ 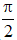+ kπ (k ∈ Z)

- Ví dụ minh họa:

Ví dụ 1. Tìm tập xác định của hàm số sau

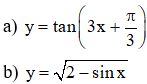
Lời giải

a)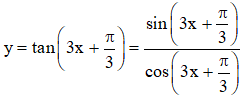

Điều kiện xác định: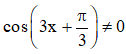

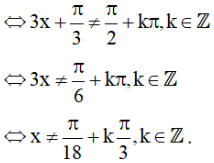
Vậy tập xác định của hàm số là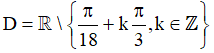

b) Điều kiện xác định: 2 - sin x ≥ 0

⇔ sin x ≤ 2 (đúng ∀x ∈ R ) vì -1 ≤ sin x ≤ 1 ∀x ∈ R

Vậy tập xác định của hàm số là D = R.

Ví dụ 2. Tìm tập xác định của hàm số sau

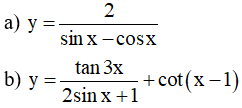
Lời giải

a) Điều kiện xác định: sin x - cos x ≠ 0 ⇔ sin x ≠ cos x (*)

+ Trường hợp 1: cosx = 0. Ta có sin²x + cos²x = 1 ⇔ sin² x = 1 ⇔ sin x = ±1.

Hiển nhiên sin x ≠ cos x

+ Trường hợp 2: cos x ≠ 0. Chia cả hai vế cho cosx

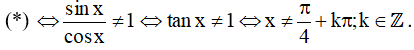
Vậy tập xác định của hàm số là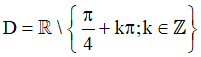

b) Vì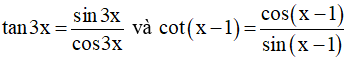

Điều kiện xác định: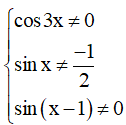

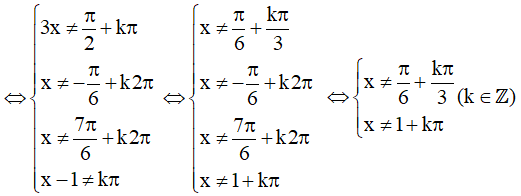
Vậy tập xác định của hàm số là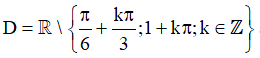

Dạng 2. Tìm tập giá trị của hàm số lượng giác

- Phương pháp giải:

Sử dụng tính bị chặn của hàm số lượng giác

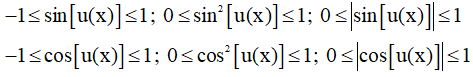
- Ví dụ minh họa:

Ví dụ 1. Tìm tập giá trị của các hàm số sau:

a) y = 2sin3x – 5

b) y = 2sin²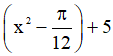

c) y = |cos(3x-2)| + 4

Lời giải

a) Ta có:

-1 ≤ sin 3x ≤ 1 ∀x ∈ R

⇔ -2 ≤ 2sin 3x ≤ 2 ∀x ∈ R

⇔ -7 ≤ 2sin 3x - 5 ≤ -3 ∀x ∈ R

Vậy tập giá trị: T = [-7;-3].

b) Ta có: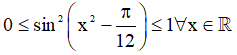

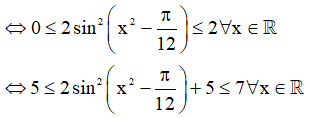
Vậy tập giá trị: T = [5;7].

c) Ta có: 0 ≤ |cos(3x - 2)| ≤ 1∀x ∈ R

⇔ 4 ≤ |cos(3x - 2)| + 4 ≤ 5∀x ∈ R

Vậy tập giá trị: T = [4;5].

Ví dụ 2. Tìm tập giác trị của các hàm số sau:

a)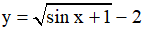

b) y = cos2x + 4sinx +1

Lời giải

a) Điều kiện xác định: sinx +1 ≥ 0 ⇔ sinx ≥ -1∀x ∈ R.

Tập xác định D = R.

Ta có: -1 ≤ sin x ≤ 1 ∀x ∈ R

⇔ 0 ≤ sinx + 1 ≤ 2 ∀x ∈ R

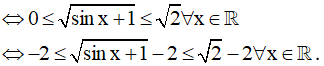
Vậy tập giá trị: T = [-2,√2 - 2 ]

b) y = cos2x + 4sinx +1 = 1 - 2sin²x + 4sinx +1 = -2sin²x + 4sinx + 2 = -2(sinx – 1)² + 4.

Ta có: -1 ≤ sin x ≤ 1 ∀x ∈ R

⇔ -2 ≤ sin x - 1 ≤ 0 ∀x ∈ R

⇔ 0 ≤ (sin x - 1)² ≤ 4 ∀x ∈ R

⇔ -8 ≤ -2(sin x - 1)² ≤ 0 ∀x ∈ R

⇔ -4 ≤ -2(sin x - 1)² + 4 ≤ 4 ∀x ∈ R .

Vậy tập giá trị: T = [-4;4].

Dạng 3. Tìm m để hàm số lượng giác có tập xác định là R

- Phương pháp giải:

m ≥ f(x) ∀x ∈ [a,b] => m ≥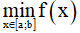

m > f(x) ∀x ∈ [a,b] => m >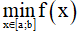

m ≤ f(x) ∀x ∈ [a,b] => m ≤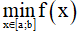

m < f(x) ∀x ∈ [a,b] => m <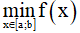

- Ví dụ minh họa:

Ví dụ 1. Tìm m để hàm số 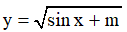xác định trên R.

Lời giải

Để hàm số xác định trên R thì sin x + m ≥ 0 ∀x ∈ R ⇔ -sin x∀x ∈ R .

Mà ta có -1 ≤ sin x ≤ 1 ∀x ∈ R ⇔ -1 ≤ -sin x ≤ 1 ∀x ∈ R

Nên m ≥ 1

Ví dụ 2. Tìm m để hàm số 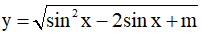xác định trên R.

Lời giải

Ta có: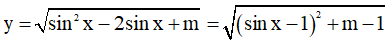

Hàm số xác định trên R khi (sinx – 1)² + m - 1 ≥ 0 ∀x ∈ R ⇔ m ≥ 1 - (sinx – 1)² ∀x ∈ R

Ta có:

-1 ≤ sin x ≤ 1 ∀x ∈ R

⇔ -2 ≤ sin x - 1 ≤ 0 ∀x ∈ R

⇔ 0 ≤ (sinx – 1)² ≤ 4 ∀x ∈ R

⇔ -4 ≤ -(sinx – 1)² ≤ 0 ∀x ∈ R

⇔ -3 ≤ 1 - (sinx – 1)² ≤ 1 ∀x ∈ R

Vậy m ≥ 1

3. Bài tập tự luyện

Câu 1. Tập xác định của hàm số 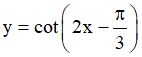là

Câu 2. Tập xác định của hàm số y = tan x + cot x là

Câu 3. Tập xác định của hàm số 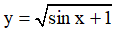là:

A. D = [ -1,+∞) B. D = R

C. D = R \ 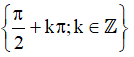D. D = (-∞, -1]

Câu 4. Tập xác định của hàm số 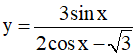là:

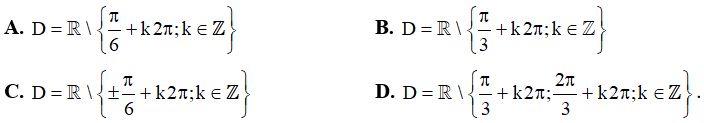
Câu 5. Tập xác định của hàm số 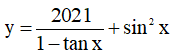là

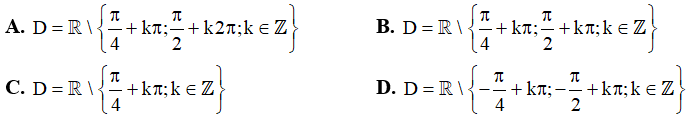
Câu 6. Tập xác định của hàm số 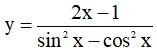là

Câu 7. Tập xác định của hàm số 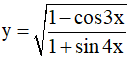là

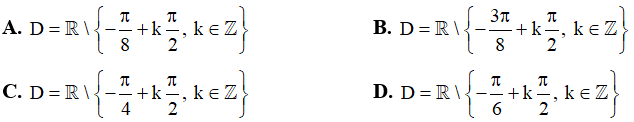
Câu 8. Hàm số nào dưới đây có tập xác định là R?

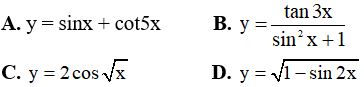
Câu 9. Tập giá trị của hàm số y = 1 – 2|sin2x| là

A. [1;3] B. [-1;1] C. [-1;3] D. [-1;0]

Câu 10. Tập giá trị của hàm số 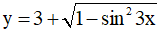là

A. [2;3] B. [1;2] C. [2;4] D. [3;4]

Câu 11. Tập giá trị của hàm số y = 2 + sinxcosx có dạng T = [m,M]. Giá trị của m là:

Câu 12. Tập giá trị của hàm số y = 2sin3x +1 là

A. [-1;1] B. [-5;7] C. [0;2] D. [-1;3]

Câu 13. Tìm m để hàm số 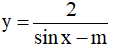xác định trên R.

A. m ∈ (-∞; -1) ∪ (1, +∞) B. m ∈ (-∞; -1] ∪ [1, +∞)

C. m ≠ 1 D. m ∈ [-1;1]

Câu 14. Hàm số 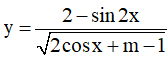có tập xác định R khi và chỉ khi:

A. m > 3 B. m < -1 C. m ≥ 3 D. m ≤ -1

Câu 15. Tìm tất cả các giá trị của tham số m để hàm số 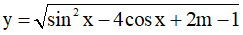có tập xác định là R.

A. 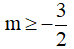B. 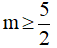C. Không có m thỏa mãn D. m ≥ 5

Bảng đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
A	D	B	C	B	C	A	D	B	D	B	D	A	A	B