Tất tần tật về phương trình bậc nhất đối với hàm số lượng giác

---

Tất tần tật về phương trình bậc nhất đối với hàm số lượng giác

Với Tất tần tật về phương trình bậc nhất đối với hàm số lượng giác Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập về phương trình bậc nhất đối với hàm số lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

1. Lý thuyết

Nhắc lại công thức nghiệm phương trình lượng giác

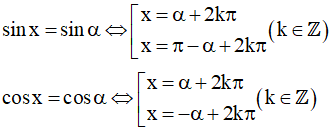
tanx = tan α ⇔ x = α + kπ(k ∈ Z)

cotx = cot α ⇔ x = α + kπ(k ∈ Z)

2. Các dạng bài tập

Dạng 1: Phương trình lượng giác sử dụng phân tích đa thức thành nhân tử đưa về phương trình tích

Phương pháp giải:

Sử dụng các biến đổi thích hợp để xuất hiện nhân tử chung như công thức nhân đôi, công thức nhân ba...

- Công thức nhân đôi:

sin2a = 2sina.cosa

cos2a = cos²a – sin²a = 2cos²a – 1 = 1 – 2sin²a

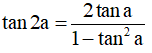
- Công thức nhân ba:

sin3a = 3sina – 4sin³a

cos3a = 4cos³a – 3cosa

Ví dụ minh họa:

Ví dụ 1: Giải các phương trình sau:

a) cosx – 2sin2x = 0

b) 6sin4x + 5sin8x = 0

c) cos²x – sin2x = 0

Lời giải

a) cosx – 2sin2x = 0

⇔ cosx - 2.2.sinxcosx = 0

⇔ cosx(1 - 4sinx) = 0

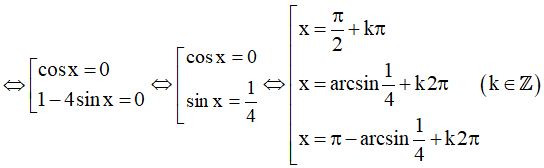
Vậy họ nghiệm của phương trình là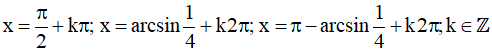

b) 6sin4x + 5sin8x = 0

⇔ 6sin4x + 5.2.sin4xcos4x = 0

⇔ 2sin4x(3 + 5cos4x) = 0

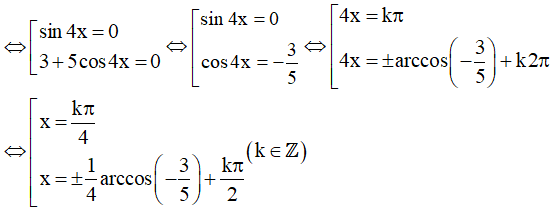
Vậy họ nghiệm của phương trình là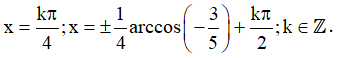

c) cos²x – sin2x = 0

⇔ cos²x – 2sinxcosx = 0

⇔ cosx(cos x - 2sinx) = 0

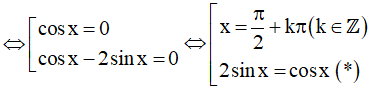
Giải phương trình (*)

Trường hợp 1: cosx = 0. Thay vào (*) ta được sinx = 0

Ta thấy sin²x + cos²x = 0² + 0² = 0 (Vô lí) (Loại).

Trường hợp 2: cosx ≠ 0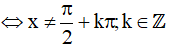

Chia hai vế của phương trình cho cosx, ta được

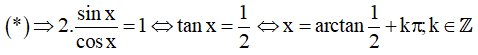(Thỏa mãn)

Vậy họ nghiệm của phương trình là: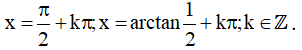

Ví dụ 2: Giải phương trình: sinx.cos3x – sinx + 2cos3x – 2 = 0.

Lời giải

Ta có: sinx.cos3x – sinx + 2cos3x – 2 = 0

⇔ sinx(cos3x - 1) + 2(cos3x - 1) = 0

⇔ (cos3x - 1)(sinx + 2) = 0

.

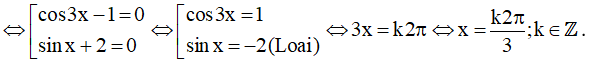Vậy họ nghiệm của phương trình là: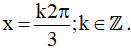

Dạng 2: Sử dụng công thức biến đổi tổng thành tích và tích thành tổng

Phương pháp giải:

- Công thức biến đổi tổng thành tích

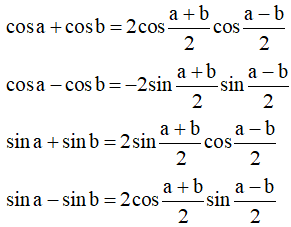
- Công thức biến đổi tích thành tổng

cosa.cosb = 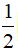[cos(a + b) + cos(a + b)]

sina.sinb = 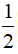[cos(a - b) - cos(a + b)]

sina.cosb = 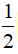[sin(a + b) + sin(a - b)]

Ví dụ minh họa:

Ví dụ 1: Giải các phương trình sau:

a) sin2x.sin5x = sin3x.sin4x

b) sin5x.cos3x = sin4x.cos2x

Lời giải

a) sin2x.sin5x = sin3x.sin4x

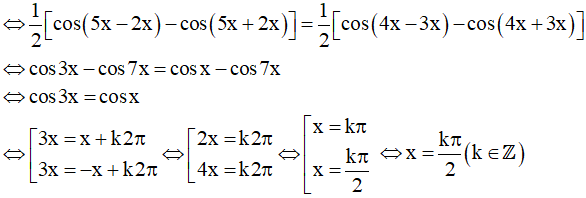
Vậy họ nghiệm của phương trình là: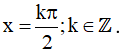

b) sin5x.cos3x = sin4x.cos2x

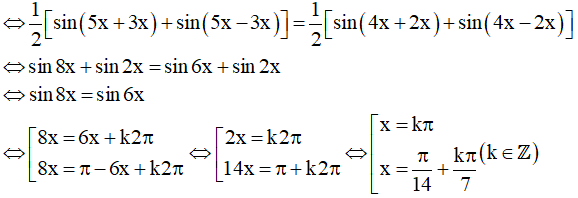
Vậy họ nghiệm của phương trình là: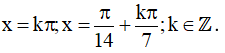

Ví dụ 2: Giải các phương trình sau:

a) sin3x + sin2x = sinx

b) sinx + sin3x = cos2x + cos4x

Lời giải

a) sin3x + sin2x = sinx

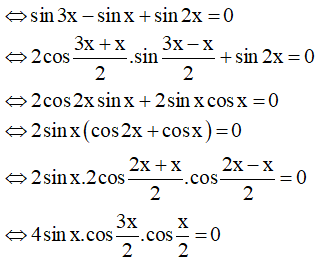
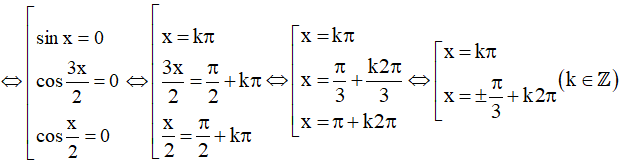
Vậy họ nghiệm của phương trình là: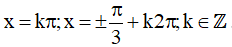

b) sinx + sin3x = cos2x + cos4x

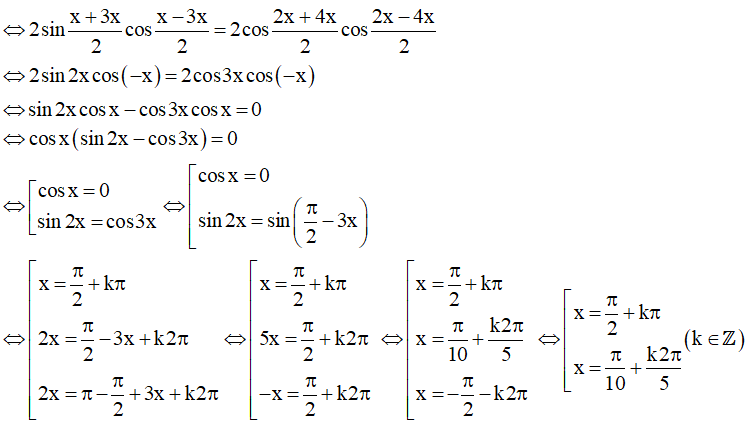
Vậy họ nghiệm của phương trình là: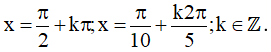

Dạng 3: Sử dụng công thức hạ bậc

Phương pháp giải:

Công thức hạ bậc hai:

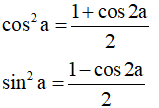
Ví dụ minh họa:

Ví dụ 1: Giải phương trình sau: sin²x + sin²3x = 2sin²2x.

Lời giải

Ta có: sin²x + sin²3x = 2sin²2x

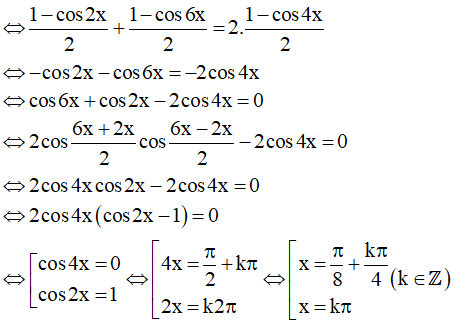
Vậy họ nghiệm của phương trình là: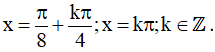

Ví dụ 2: Giải phương trình sau: cos²x + cos²2x + cos²3x + cos²4x = 2

Lời giải

Ta có: cos²x + cos²2x + cos²3x + cos²4x = 2

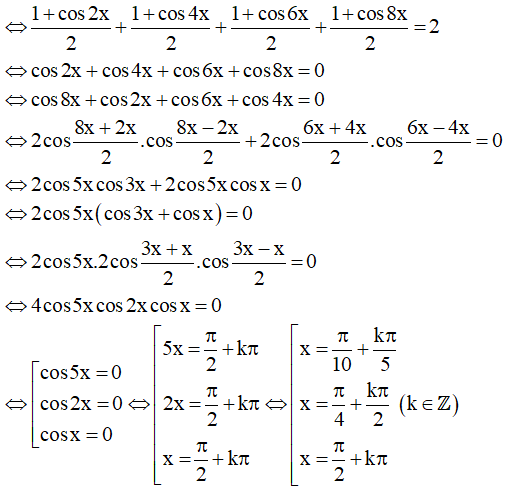
Vậy họ nghiệm của phương trình là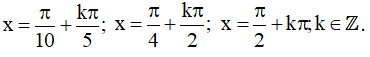

3. Bài tập tự luyện

Câu 1. Nghiệm của phương trình cos²x – cosx = 0 thuộc khoảng 0 < x < π là:

Câu 2. Giải phương trình cos²x – sin2x = 0

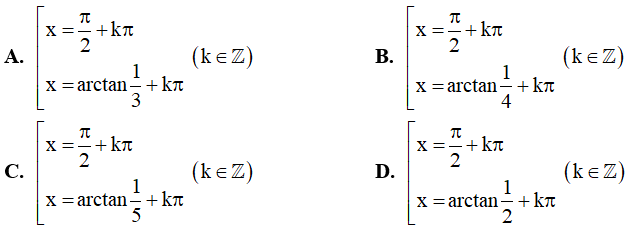
Câu 3. Nghiệm của phương trình sin2x – sinx = 2 – 4cosx là:

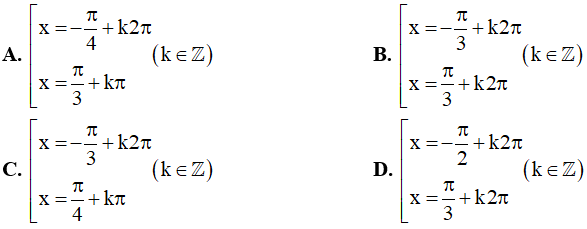
Câu 4. Nghiệm của phương trình sin x.cos x.cos2x = 0 là:

Câu 5. Nghiệm của phương trình cos3x – cos5x = sinx là:

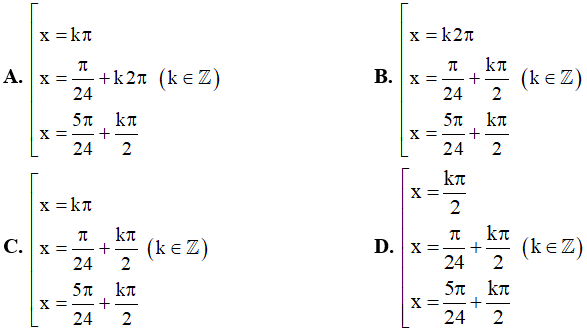
Câu 6. Phương trình cos5x.cos3x = cos 4x.cos2x có tập nghiệm trùng với tập nghiệm của phương trình nào sau đây?

A. sinx = cos x B. cosx = 0 C. cos8x = cos6x D. sin8x = cos6x

Câu 7. Phương trình cosx + 3cos2x + cos3x = 0 có nghiệm là:

Câu 8. Nghiệm của phương trình cos3x – cos4x + cos5x = 0 là:

Câu 9. Phương trình 2sinx + cosx – sin2x – 1 = 0 có nghiệm là:

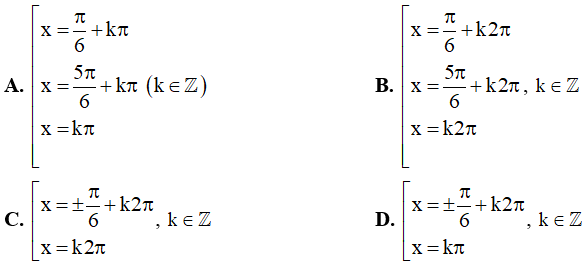
Câu 10. Một họ nghiệm của phương trình cos x.sin²3x – cosx = 0 là :

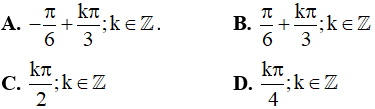
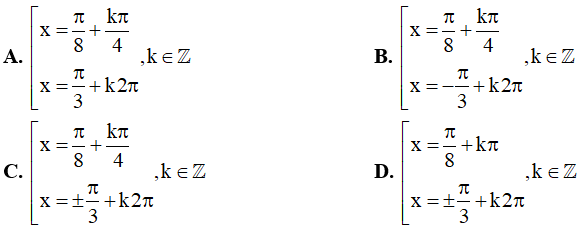
Câu 11. Các nghiệm của phương trình sin²x + sin²3x = cos²x + cos²3x là:

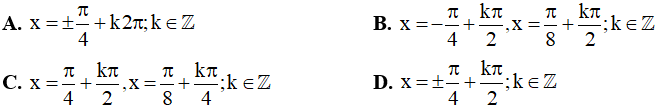
Câu 12. Các nghiệm của phương trình 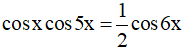(với k ∈ Z ) là:

Câu 13. Họ nghiệm của phương trình sin²x + cos²4x = 1 là:

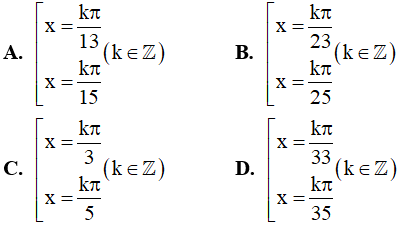
Câu 14. Họ nghiệm của phương trình cosx.cos7x = cos3x.cos5x là:

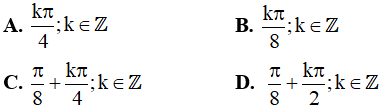
Câu 15. Phương trình sin²3x – cos²4x = sin²5x – cos²6x có các nghiệm là:

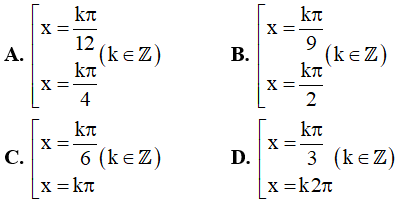
Bảng đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
B	D	B	D	C	C	C	C	B	B	C	D	C	A	B