Phương pháp tính giá trị lớn nhất – giá trị nhỏ nhất của hàm số lượng giác

---

Phương pháp tính giá trị lớn nhất – giá trị nhỏ nhất của hàm số lượng giác

Với Phương pháp tính giá trị lớn nhất – giá trị nhỏ nhất của hàm số lượng giác Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính giá trị lớn nhất – giá trị nhỏ nhất của hàm số lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

1. Lý thuyết

a) Cho hàm số y = f(x) xác định trên miền D ⊂ R .

- Số thực M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu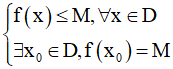

- Số thực m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu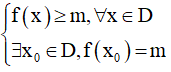

b) Tính bị chặn của hàm số lượng giác:

-1 ≤ sin x ≤ 1∀x ∈ R

-1 ≤ cos x ≤ 1∀x ∈ R

2. Các dạng bài tập

Dạng 1. Sử dụng tính bị chặn của hàm số lượng giác

Phương pháp giải:

-1 ≤ sin [u(x)] ≤ 1; 0 ≤ sin²[u(x)] ≤ 1; 0 ≤ |sin[u(x)]| ≤ 1

-1 ≤ cos [u(x)] ≤ 1; 0 ≤ cos²[u(x)] ≤ 1; 0 ≤ |cos[u(x)]| ≤ 1

Ví dụ minh họa:

Ví dụ 1: Tìm giá trị lớn nhất và nhỏ nhất của các hàm số:

a) y = sin2x + 3

b) y = 4sin2xcos2x +1

c) y = 5 – 3cos²3x

Lời giải

a) Ta có: -1 ≤ sin 2x ≤ 1 ∀x ∈ R

⇔ 2 ≤ sin 2x + 3 ≤ 4 ∀x ∈ R

Vậy hàm số y = sin2x + 3 có giá trị lớn nhất là 4 và giá trị nhỏ nhất là 2.

b) y = 4sin2xcos2x +1 = 2sin4x + 1

Ta có: -1 ≤ sin 4x ≤ 1 ∀x ∈ R

⇔ -2 ≤ 2sin 4x ≤ 2 ∀x ∈ R

⇔ -1 ≤ 2sin 4x + 1 ≤ 3 ∀x ∈ R

Vậy hàm số y = 4sin2xcos2x +1 có giá trị lớn nhất là 3 và giá trị nhỏ nhất là -1.

c) Ta có: 0 ≤ cos²3x ≤ 1 ∀x ∈ R

⇔ 0 ≤ 3cos²3x ≤ 3 ∀x ∈ R

⇔ -3 ≤ -3cos²3x ≤ 0 ∀x ∈ R

⇔ 2 ≤ 5 - 3cos²3x ≤ 5 ∀x ∈ R

Vậy hàm số y = 5 – 3cos²3x có giá trị lớn nhất là 5 và giá trị nhỏ nhất là 2.

Ví dụ 2: Tìm giá trị lớn nhất và nhỏ nhất của các hàm số:

a) y =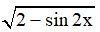

b) y = cos2x + 4sinx - 5

c) y = 4|cos(3x-1)| + 1

Lời giải

a) Điều kiện xác định: 2 - sin2x ≥ 0 ⇔ sin 2x ≤ 2 (Luôn đúng với mọi x)

Tập xác định D = R.

Ta có: -1 ≤ sin 2x ≤ 1 ∀x ∈ R

⇔ -1 ≤ -sin 2x ≤ 1 ∀x ∈ R

⇔ 1 ≤ 2 - sin 2x ≤ 3 ∀x ∈ R

⇔ 1 ≤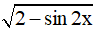≤ √3∀x ∈ R

Vậy hàm số y = 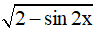có giá trị lớn nhất là √3 và giá trị nhỏ nhất là 1.

b) y = cos2x + 4sinx – 5

= 1 – 2sin²x + 4sinx – 5

= -2sin²x + 4sinx – 4

= -2(sin²x – 2sinx + 1) – 2

= -2(sinx – 1)² – 2

Ta có: -1 ≤ sinx ≤ 1 ∀x ∈ R

⇔ -2 ≤ sinx - 1 ≤ 0 ∀x ∈ R

⇔ 0 ≤ (sinx - 1)² ≤ 4 ∀x ∈ R

⇔ -8 ≤ -2(sinx - 1)² ≤ 0 ∀x ∈ R

⇔ -10 ≤ -2(sinx - 1)² - 2 ≤ -2 ∀x ∈ R

Vậy hàm số y = cos2x + 4sinx – 5 có giá trị lớn nhất là -2 và giá trị nhỏ nhất là -10.

c) Ta có: 0 ≤ |cos(3x-1)| ≤ 1 ∀x ∈ R

⇔ 0 ≤ 4|cos(3x-1)| ≤ 4 ∀x ∈ R

⇔ 1 ≤ 4|cos(3x-1)| + 1≤ 5 ∀x ∈ R

Vậy hàm số y = 4|cos(3x-1)| + 1 có giá trị lớn nhất là 5 và giá trị nhỏ nhất là 1.

Dạng 2. Hàm số có dạng y = asinx + bcosx + c (với a, b khác 0)

Phương pháp giải:

Bước 1: Ta đưa hàm số về dạng chỉ chứa sin[u(x)] hoặc cos[u(x)]:

y = asinx + bcosx + c =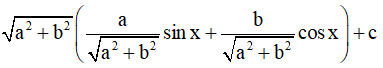

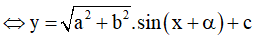với α thỏa mãn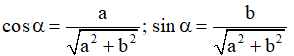

Bước 2: Đánh giá -1 ≤ sin (x + α) ≤ 1 ∀x ∈ R

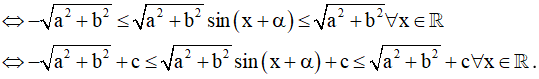
Ví dụ minh họa:

Ví dụ 1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số:

a) y = sin2x - √3cos2x + 1

b) y = 3sinx + 4cosx + 6

Lời giải

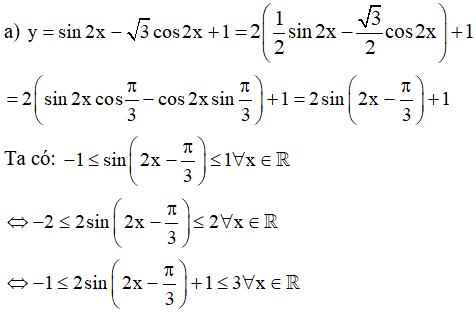
Vậy hàm số y = sin2x - √3cos2x + 1 có giá trị lớn nhất là 3 và giá trị nhỏ nhất là -1.

b) y = 3sinx + 4cosx + 6 =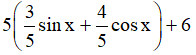

Đặt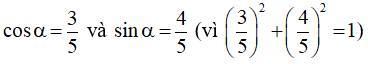

Ta được: y = 5(sinxcosα + cosxsinα) + 6 = 5(sinx + α) + 6

Ta có: -1 ≤ sin (x + α) ≤ 1 ∀x ∈ R

⇔ -5 ≤ 5sin (x + α) ≤ 5 ∀x ∈ R

⇔ 1 ≤ 5sin (x + α) + 6 ≤ 11 ∀x ∈ R

Vậy hàm số y = 3sinx + 4cosx + 6 có giá trị lớn nhất là 11 và giá trị nhỏ nhất là 1.

Ví dụ 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số √3sin2x + sin²x - cos²x + 1

Lời giải

y = √3sin2x + sin²x - cos²x + 1

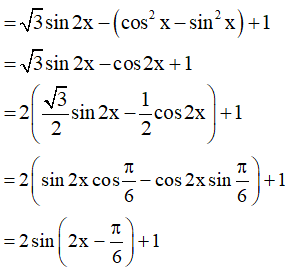
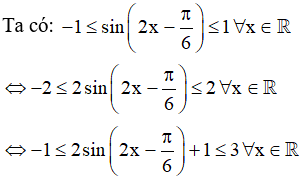
Vậy hàm số có giá trị lớn nhất là 3 và giá trị nhỏ nhất là -1.

Dạng 3: Hàm số có dạng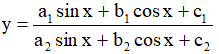

Lý thuyết: Phương trình asinx + bcosx = c có nghiệm khi a² + b² ≥ c² (Lý thuyết có trong phần 7)

Phương pháp giải:

Bước 1: Điều kiện xác định: a₂sinx + b₂cosx = c₂ ≠ 0

Bước 2: 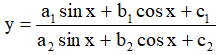⇔ ya₂sinx + yb₂cosx + yc₂ = a₁sinx + b₁cosx + c₁

⇔ (ya₂ - a₁)sinx + (yb₂ - b₁)cosx = -yc + c₁ (*)

Bước 3: Để phương trình (*) có nghiệm x thì (ya₂ - a₁)² + (yb₂ - b₁)² ≥ (-yc + c₁)²

Tìm đoạn chứa y, sau đó đưa ra kết luận về giá trị lớn nhất và giá trị nhỏ nhất.

Ví dụ minh họa:

Ví dụ 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: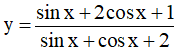

Lời giải

Điều kiện xác định: sinx + cosx + 2 ≠ 0

Ta có: sinx + cosx + 2 = .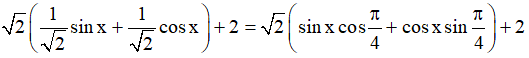

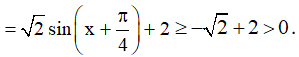Do đó sinx + cosx + 2 ≠ 0 ∀x∈ R

Tập xác định: D = R.

Ta có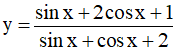

⇔ ysinx + ycosx + 2y = sinx + 2cosx + 1

⇔ (y - 1)sinx + (y - 2)cosx = 1 - 2y (*)

Để phương trình (*) có nghiệm x thì (y - 1)² + (y - 2)² ≥ (1 - 2y)²

⇔ y² - 2y + 1 + y² - 4y + 4 ≥ 1 - 4y + 4y²

⇔ 2y² + 2y - 4 ≤ 0

⇔ 2(y - 1)(y + 2) ≤ 0

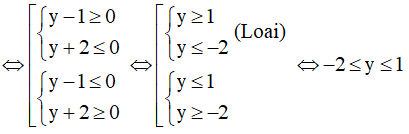
Vậy hàm số có giá trị lớn nhất là 1 và giá trị nhỏ nhất là -2.

Ví dụ 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: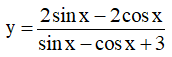

Lời giải

Điều kiện xác định: sinx – cosx + 3 ≠ 0

Ta có: sinx – cosx + 3 = .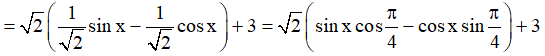

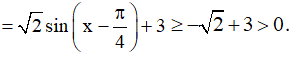Do đó sinx – cosx + 3 ≠ 0 ∀x ∈ R

Tập xác định: D = R.

Ta có: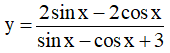

⇔ ysinx - ycosx + 3y = 2sinx - 2cosx

⇔ (y - 2)sinx - (y + 2)cosx = - 3y (*)

Để phương trình (*) có nghiệm x thì (y - 2)² + (y + 2)² ≥ (-3y)²

⇔ y² - 4y + 4 + y² + 4y + 4 ≥ 9y²

⇔ 7y² ≤ 8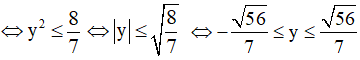

Vậy hàm số có giá trị lớn nhất là 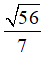và giá trị nhỏ nhất là - .

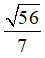3. Bài tập tự luyện

Câu 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=2sin5x – 1

A. min y = -3, max y = 3 B. min y = -1, max y = 1

C. min y = -1, max y=3 D. min y = -3, max y = 1

Câu 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 1 + cos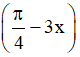

A. min y = -2, max y = 4 B. min y = 2, max y = 4

C. min y = -2, max y = 3 D. min y = -1, max y = 4

Câu 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số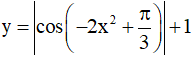

A. max y = 1, min y = 0 B. max y = 2, min y = 0

C. max y = 1, min y = -1 D. max y = 2, min y = 1

Câu 4. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số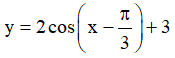

A. min y = 2, max y = 5 B. min y = 1, max y = 4

C. min y = 1,max y = 5 D. min y = 1, max y = 3

Câu 5. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

A. max y = √5, min y = 1 B. max y = √5 , min y = 2√5

C. max y = √5, min y = 2 D. max y = √5 , min y = 3

Câu 6. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số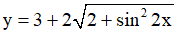

A. min y = 3 + 2√2 , max y = 3 + 2√3 B. min y = 2 + 2√2 , max y = 3 + 2√3

C. min y = 3 - 2√2 , max y = 3 + 2√3 D. min y = 3 + 2√2 , max y = 3 + 3√3

Câu 7. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3 – 2cos²3x

A. min y = 1, max y = 2 B. min y = 1, max y = 3

C. min y = 2, max y = 3 D. min y = -1, max y = 3

Câu 8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = sin²x – 4sinx + 5

A. max y = 9, min y = 2 B. max y = 10, min y = 2

C. max y = 6, min y = 1 D. max y = 5, min y = 1

Câu 9. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = cos2x + 4cosx – 2

A. max y = 3, min y = -7 B. max y = -1, min y = -5

C. max y = 4, min y = -1 D. max y = 3, min y = -5

Câu 10. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3sin x + 4cosx + 1

A. max y = 6, min y = -2 B. max y = 4, min y = -4

C. max y = 6, min y = -4 D. max y = 6, min y = -1

Câu 11. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = √3 cosx + sinx + 4

A. min y = 2, max y = 4 B. min y = 2, max y = 6

C. min y = 4, max y = 6 D. min y = 2, max y = 8

Câu 12. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 4sin 6x + 3cos 6x

A. min y = -5, max y = 5 B. min y = -4, max y = 4

C. min y = -3, max y = 5 D. min y = -6, max y = 6

Câu 13. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 2sin²x + 3sin2x – 4cos²x

A. min y = -3√2 - 1, max y = 3√2 + 1 B. min y = -3√2 - 1, max y = 3√2 - 1

C. min y = -3√2, max y = 3√2 - 1 D. min y = -3√2 - 2, max y = 3√2 - 1

Câu 14. Giá trị lớn nhất của hàm số 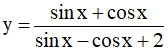là

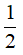A. 1 B. √2 C. D. 2

Câu 15. Gọi M, m lần lượt là giá trị nhỏ nhất của hàm số 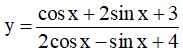. Giá trị của M+m là:

Bảng đáp án

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
D	A	D	C	A	A	B	B	D	C	B	A	B	A	B