Phương trình bậc nhất đối với hàm số lượng giác - Toán lớp 11

---

Phương trình bậc nhất đối với hàm số lượng giác

Với Phương trình bậc nhất đối với hàm số lượng giác Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phương trình bậc nhất đối với hàm số lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

+ Định nghĩa: Phương trình bậc nhất đối với một hàm số lượng giác là có dạng:

a. sinx + b= 0 ( trong đó a ≠ 0) hoặc ( a.cosx+b= 0; a.tan x+ b= 0; a.cotx+ b= 0)

+ Để giải được phương trình bậc nhất đối với một hàm số lượng giác ta làm như sau:

• Bước 1: Đưa phương trình về dạng: sinx= m ( hoặc cosx =m; tanx= m; cotx= m).

• Bước 2. Giải phương trình lượng giác cơ bản.

• Bước 3. Kết luận nghiệm của phương trình đã cho.

B. Ví dụ minh họa

Ví dụ 1. Nghiệm của phương trình √12+2tanx=0 là:

A. π/6+kπ

B. (-π)/3+kπ

C. (-π)/6+kπ

D. (-π)/6+k2π

Lời giải

Chọn C

Ta có: √12+2tanx=0 ⇔ 2√3+2tanx=0

⇔ tan x= - √3 ⇔ tanx= tan (- π)/3

⇔ x= (-π)/3+kπ

Ví dụ 2. Tìm nghiệm của phương trình: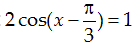

A.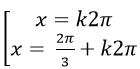

B.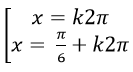

C.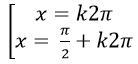

D.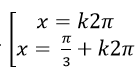

Lời giải

Chọn A.

Ta có:

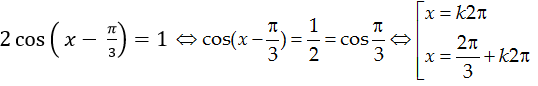
Ví dụ 3. Cho phương trình 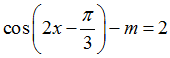. Tìm m để phương trình có nghiệm?

A. Không tồn tại m.

B.m ϵ[-1;3] .

C. m ϵ[-3;-1]

D. mọi giá trị của m.

Lời giải

Chọn C.

Ta có: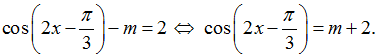

Với mọi x ta luôn có: - 1 ≤ cos⁡( 2x- π/3) ≤ 1

Do đó phương trình có nghiệm khi và chỉ khi:

-1 ≤ m+2 ≤ 1 hay-3 ≤ m ≤ -1

Ví dụ 4: Họ nghiệm của phương trình cot(x+π/3)+1=0 là

A. .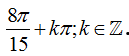

B.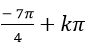

C. .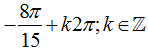

D.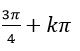

Lời giải

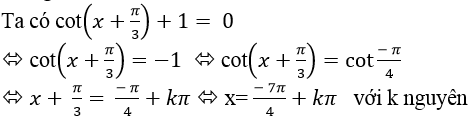
Chọn B.

Ví dụ 5: Nghiệm của phương trình 3cot x+ √3=0là:

A.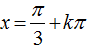

B.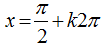

C.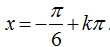

D. x= (-π)/3+kπ.

Lời giải

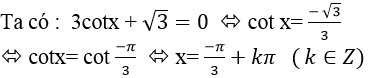
Chọn D.

Ví dụ 6: Phương trình 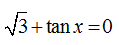có nghiệm là

A.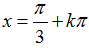

B.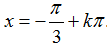

C.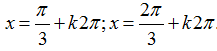

D.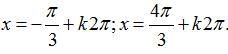

Lời giải

Ta có: √3+tanx=0

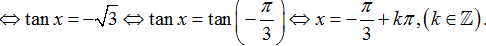
Chọn B.

Ví dụ 7: Giải phương trình : 2tanx+ 10= 0

A. x= arctan 5+ k.π

B. x = arctan -5+ kπ

C. x= - 5+kπ

D. x= 1/5+kπ

Lời giải

Ta có: 2tanx + 10 = 0 ⇒ 2tanx= - 10

⇒ tanx= - 5.

Sử dụng công thức nghiệm tổng quát của phương trình

Suy ra:Nghiệm của phương trình đã cho là: x= arctan-5+ kπ; k∈Z

Ví dụ 8: Giải phương trình : 1/2.cot⁡( x+3π/4)=0.

A. (-π)/4+kπ.

B. π/4+kπ.

C. π/2+kπ.

D. π/3+kπ

Lời giải

Ta có: 1/2.cot⁡( x+3π/4)=0 ⇒ cot⁡( x+3π/4)=0.

⇒ cot(x+ 3π/4)=cot π/2

⇒ x+ 3π/4= π/2+kπ ⇒ x= (-π)/4+kπ

Chon A.

Ví dụ 9: Nghiệm của phương trình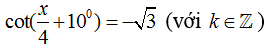

A. .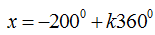

B. .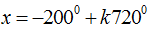

C. .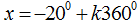

D. .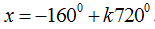

Lời giải

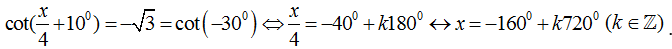
Chọn D.

Ví dụ 10. Giải phương trình : 2cos(x+ 30⁰) + 1= 0

A.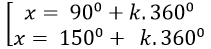

B.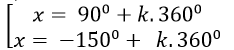

C.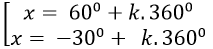

D.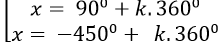

Lời giải

Ta có: 2cos(x+30⁰)+ 1= 0 ⇒ 2cos(x+ 30⁰) = - 1

⇒ cos( x+ 30⁰)= -1/2 = cos120⁰

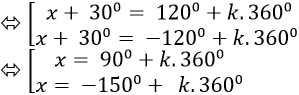
Chọn B.

Ví dụ 11: Giải phương trình : 2sin( x – 10⁰) – sin90⁰ = 0

A.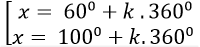

B.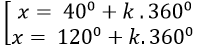

C.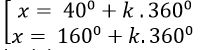

D. Một đáp án khác

Lời giải

Ta có: 2sin(x- 10⁰) - sin 90⁰= 0

⇒ 2sin(x – 10⁰) = sin90⁰ = 1

⇒ sin( x- 10⁰) = 1/2 = sin30⁰

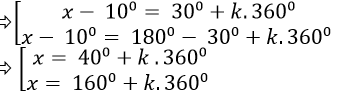
Chọn C.

Ví dụ 12.Giải phương trình 2cos(x+ 10⁰) + 10= 0

Lời giải

Ta có : 2cos(x+ 10⁰) + 10= 0

⇒ 2cos(x+ 10⁰) = - 10

⇒ cos( x+ 10⁰) = - 5 (*)

Do với mọi x ta luôn có: - 1 ≤ cos⁡(x+ 10⁰ ) ≤ 1 nên từ (*) suy ra phương trình (*) vô nghiệm.

Vậy phương trình đã cho vô nghiệm.

C. Bài tập vận dụng

Câu 1:Giải phương trình 2cos( 120⁰ - x)+ 1= 0

A.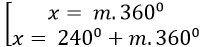

B.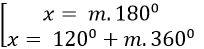

C.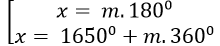

D.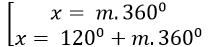

Lời giải:

Ta có: 2cos (120⁰- x) + 1 = 0

⇒ 2cos(120⁰ – x) = - 1

⇒ cos(120⁰-x) = (- 1)/2=cos120⁰

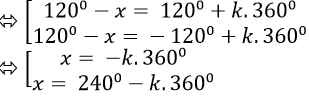
Vậy phương trình đã cho có nghiệm là: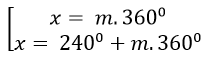

Câu 2:Giải phương trình: 3sin⁡(x- π/5)+3=0

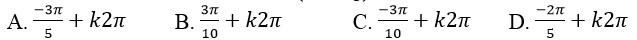
Lời giải:

Ta có: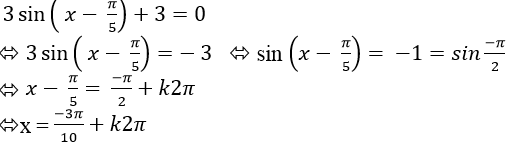

Chọn C.

Câu 3:Giải phương trình: √2 tan⁡( x- 15⁰ )- √2=0

A. 30⁰+ k. 180⁰

B.45⁰+ k.360⁰

C.45⁰+ k.180⁰

D. 60⁰+ k. 180⁰

Lời giải

Lời giải:

Ta có: √2 tan⁡( x- 15⁰ )- √2=0

⇒ √2 tan⁡( x- 15⁰ )= √2

⇒ tan (x- 15⁰) = 1= tan 45⁰

⇒ x- 15⁰ = 45⁰+ k. 180⁰

⇒ x = 60⁰+ k.180⁰

Vậy nghiệm của phương trình đã cho là x= 60⁰+ k. 180⁰

Chọn D.

Câu 4:Giải phương trình 3 cot⁡(x+ 2π/5)- √3=0

A.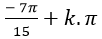

B.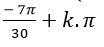

C.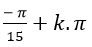

D.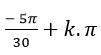

Lời giải:

Ta có:

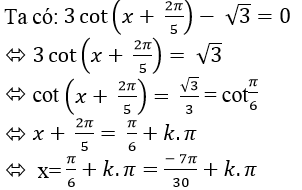
Chọn B.

Câu 5:Giải phương trình 2tanx – 6= 0

A. x= 3+ k. π

B. x = - 3+ kπ

C.x= arctan 3+ kπ

D. Phương trình vô nghiệm

Lời giải:

Ta có: 2tanx – 6= 0 ⇒ 2tanx = 6

⇒ tan x= 3

⇒ x = arcrtan 3+ k.π

Chọn C.

Câu 6:Giải phương trình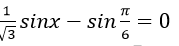

A.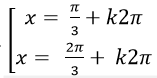

B.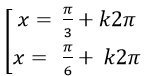

C.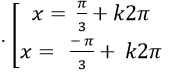

D.Phương trình vô nghiệm

Lời giải:

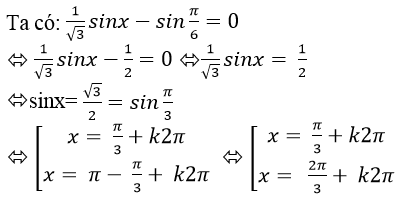
Chọn A.

Câu 7:Giải phương trình 3sin(x+ 10⁰) - 1=0

A.

B.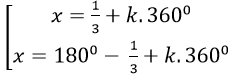

C.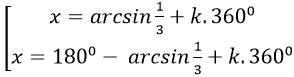

D.

Lời giải:

Ta có; 3sin(x+ 10⁰) - 1= 0

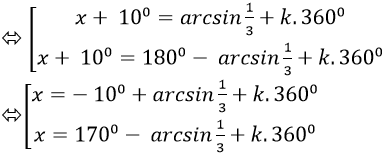
Chọn D.

Câu 8:Giải phương trình √3 sin⁡( x+π/10)+3=0

A. x= π/10+k2π

B. x= -π/10+k2π

C. Phương trình vô nghiệm

D. Đáp án khác

Lời giải:

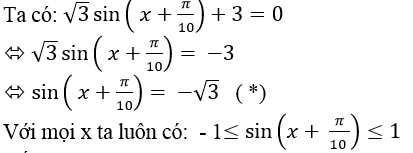
Kết hợp với (*) suy ra phương trình đã cho vô nghiệm

Chọn D.

Câu 9:Giải phương trình: 2sin( x+π/6) – cos 3π/2=0

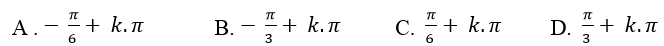
Lời giải:

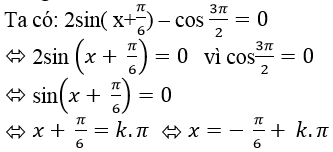
Chọn A.

Câu 10:Giải phương trình : 2sin(x+ π/8)-10=0

A.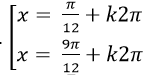

B.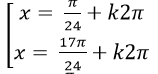

C.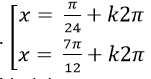

D.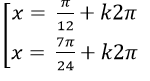

Lời giải:

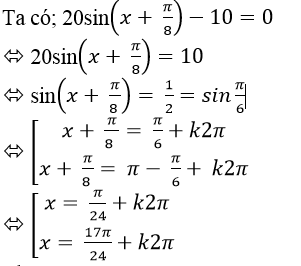
Chọn B.