Phương trình thuần nhất bậc 2 đối với sinx và cosx - Toán lớp 11

---

Phương trình thuần nhất bậc 2 đối với sinx và cosx

Với Phương trình thuần nhất bậc 2 đối với sinx và cosx Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phương trình thuần nhất bậc 2 đối với sinx và cosx từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

+ Phương trình thuần nhất bậc hai đối với sinx và cosx là phương trình có dạng:

a.sin² x+ b. sinx. cosx + c. cos² x= 0 (1)

trong đó a; b và c là các số đã cho với a ≠ 0 hoặc b ≠ 0 hoặc c ≠ 0

+Có hai cách để giải phương trình thuần nhất bậc hai đối với sinx và cosx :

* Cách 1.

Bước 1: Kiểm tra cosx = 0 có nghiệm của phương trình.

Chú ý: cosx=0 ⇒ sin² x= 1

Bước 2. Nếu cosx ≠ 0 chia cả hai vế của phương trình cho cos²x. Khi đó phương trình đã cho có dạng: a. tan² x+ b. tanx+ c= 0

Đây là phương trình bậc hai ẩn tanx. Giải phương trình ta tính được tanx

⇒ x= ....

Chú ý: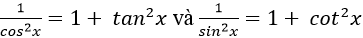

* Cách 2.Áp dụng công thức hạ bậc; công thức nhân đôi ta có:

a. sin² x+ b. sinx. cosx+ c.cos² x= 0

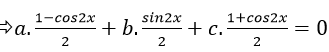
⇒ b.sin2x+( c-a) cos2x = - a- c

Đây là phương trình bậc nhất đối với sinx và cosx

B. Ví dụ minh họa

Ví dụ 1. Giải phương trình: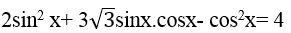

A.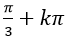

B.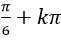

C.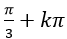

D. Vô nghiệm

Lời giải

+ Trường hợp 1.

Thay cosx = 0 vào phương trình đã cho ta thấy không thỏa mãn.

+ Trường hợp 2. Với cosx ≠ 0

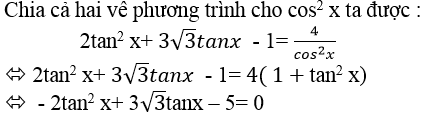
Phương trình này vô nghiệm

⇒ Phương trình đã cho vô nghiệm.

Chọn D.

Ví dụ 2: Phương trình 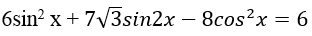có các nghiệm là:

A.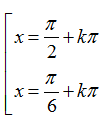

B.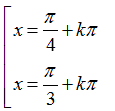

C.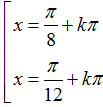

D.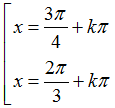

Lời giải

Trường hợp 1. Với cosx=0 ⇒ sin2x = 1 thay vào phương trình đã cho ta được :

6.1+0 – 0= 6 (luôn đúng )

⇒ phương trình có nghiệm x= π/2+kπ

Trường hợp 2. Nếu cos x ≠ 0 chia cả hai vế cho cos2x ta được

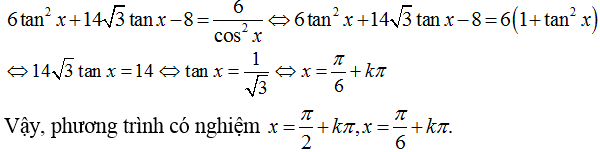
Chọn A

Ví dụ 3. Cho phương trình 2sin² x – 5sinx. cosx +3cos² x= 0. Tìm một họ nghiệm của phương trình:

A.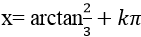

B.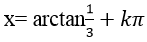

C.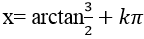

D.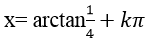

Lời giải

+ Trường hợp 1. Nếu cosx=0 ⇒ sin2 x= 1 thay vào phương trình đã cho ta thấy không thỏa mãn.

+ Trường hợp 2. Nếu cosx ≠ 0. Chia cả hai vế của phương trình cho cos² x ta được:

2tan² x – 5tanx + 3= 0

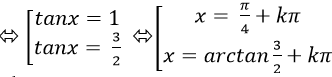
Chọn C

Ví dụ 4. Giải phương trình 4sin² x+4sinx. cosx+ cos²x= 0 .

A.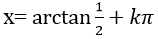

B.x= arctan⁡(-2)+kπ

C.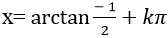

D.x= arctan⁡2+kπ

Lời giải

+ Trường hợp 1.Nếu cosx= 0 ⇒ sin² x= 1 thay vào phương trình đã cho ta thấy không thỏa mãn.

+Trường hợp 2. Nếu cosx ≠ 0. Chia cả hai vế phương trình cho cos² x ta được :

4tan² x + 4tanx +1= 0 ⇒ (2tanx+1)²= 0

⇒ 2tanx+1 = 0 ⇒ tan x= (-1)/2

⇒ x= arctan⁡(- 1)/2+kπ

Chọn C.

Ví dụ 5. Phương trình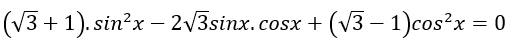 có các nghiệm là:

A .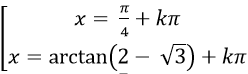

B.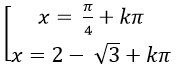

C.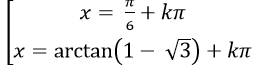

D. Tất cả sai

Lời giải

+ Trường hợp 1: Nếu cosx= 0 ⇒ sin2x = 1 thay vào phương trình đã cho ta thấy không thỏa mãn

+ trường hợp 2: Nếu cosx ≠ 0 ta chia cả hai vế của phương trình cho cos2 x ta được:

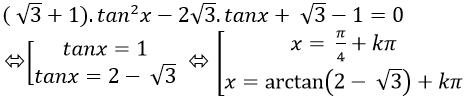
Chọn A.

Ví dụ 6: Giải phương trình - 3sin²x – 2sinx.cosx + 4cos² x= - 3

A.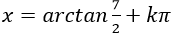

B .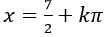

C.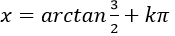

D.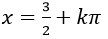

Lời giải

+ Trường hợp 1. Nếu cosx= 0 ⇒ sin² x= 1 thay vào phương trình đã cho ta thấy không thỏa mãn.

+ Trường hợp 2. Nếu cosx ≠ 0. Chia hai vế phương trình cho cos2 x ta được:

- 3tan² x -2tanx + 4= (- 3)/(cos² x)

⇒ - 3tan² x – 2tanx + 4= - 3( 1+ tan² x)

⇒ - 2tanx = -7 ⇒ tanx= 7/2

⇒ x=arctan 7/2+kπ

Chọn A.

Ví dụ 7: Phương trình 2sin² x+ sinx.cosx – cos² x= 0 có nghiệm là:

A.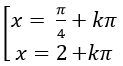

B.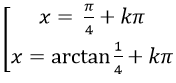

C.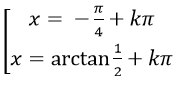

D.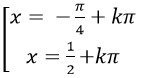

Lời giải

+ Trường hợp 1. Nếu cosx= 0 ⇒ sin² x=1 thay vào phương trình ta thấy không thỏa mãn.

+ Trường hợp 2. Nếu cosx ≠ 0; chia cả hai vế của phương trình cho cos² x ta được:

2tan² x+ tanx – 1= 0

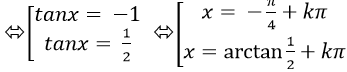
Chọn C.

Ví dụ 8: Một họ nghiệm của phương trình: 2sin²x - 5sinx.cosx–cos² x= - 2 là

A. x=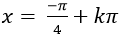

B. x=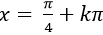

C. x=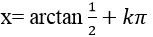

D. x=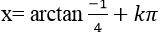

Lời giải

+ Trường hợp 1: Nếu cosx= 0 ⇒ sin² x= 1 thay vào phương trình đã cho ta thấy không thỏa mãn.

+ trường hợp 2. Nếu cosx ≠ 0 chia cả hai vế cho cos2 x ta được :

2 tan²x – 5 tanx - 1= (- 2)/(cos² x)

⇒ 2tan² x – 5tanx – 1= - 2( 1+ tan²x)

⇒ 2tan²x – 5tanx -1= - 2 – 2tan² x

⇒ 4tan² x – 5tanx + 1= 0

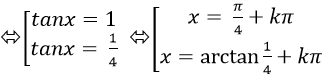
Chọn B.

Ví dụ 9. Cho phương trình : 2sin² x- 4sinx.cosx+4 cos²x= m. Tìm điều kiện của m để phương trình đã cho có nghiệm

A. 1 < m hoặc m < - 1

B.m > √3 hoặc m < - √5

C. 2- √5 ≤ m ≤ 2+ √5

D.Đáp án khác

Lời giải

Áp dụng công thức hạ bậc và công thức nhân đôi ta có:

2sin² x- 4sinx.cosx+ 4cos² x=m

⇒ (1-cos2x)-2sin2x+2cos2x+1 = m

⇒ cos2x – 2sin2x = m- 2

Đây là phương trình bậc nhất đối với sin2x và cos2x nên điều kiện để phương trình có nghiệm là: 1² + (-2)² ≥ (m-2)²

⇒ 5 ≥ m² - 4m+ 4 ⇒ m² – 4m - 1 ≤ 0

⇒ 2- √5 ≤ m ≤ 2+ √5

Chọn C.

Ví dụ 10: Giải phương trình 4sin³ x+ 3cos³x- 3sinx – sin²x.cosx= 0

A.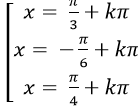

B.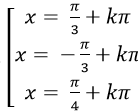

C.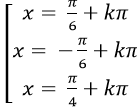

D. Đáp án khác

Lời giải

+ Trường hợp 1. Nếu cosx= 0 ⇒ sin² x= 1 thay vào phương trình đã cho ta thấy không thỏa mãn.

+ Trường hợp 2.Nếu cosx ≠ 0. Chia cả hai vế cho cos³ x ta được:

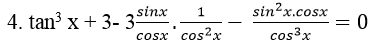
⇒ 4.tan³ x+ 3- 3tanx.(1+ tan² x) – tan²x = 0

⇒ 4.tan³ x + 3- 3tanx – 3tan³x – tan² x = 0

⇒ tan³ x – tan² x -3tanx + 3= 0

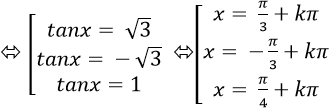
Chọn B.

Ví dụ 11: Giải phương trình 2cos³x = sin3x

A.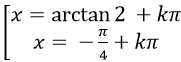

B.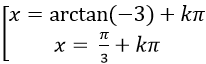

C.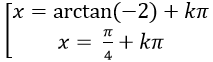

D.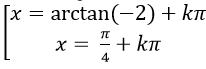

Lời giải

Ta có: 2cos³x = sin³x

⇒ 2cos³ x= 3sinx- 4sin³x

Ta thấy cosx=0 không là nghiệm của phương trình đã cho.Chia cả hai vế phương trình cho cos³ x ta được:

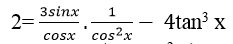
⇒ 2= 3. tanx( 1+ tan² x) – 4tan³ x

⇒ 2= 3tanx + 3tan³x – 4tan³x

⇒ tan³x – 3tanx + 2= 0

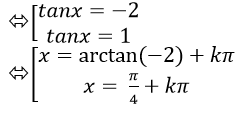
Chọn C.

Ví dụ 12: Giải phương trình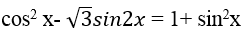

A.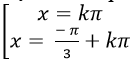

B.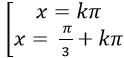

C.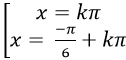

D. Đáp án khác

Lời giải

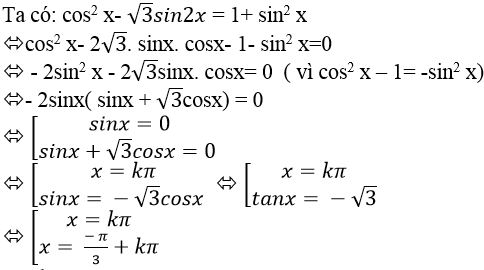
Chọn A.

C. Bài tập vận dụng

Câu 1:Giải phương trình 4sin²x+ 5sinx. cosx – 9cos² x= 0

A.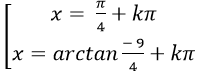

B.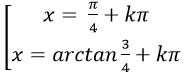

C.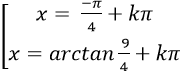

D.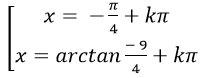

Lời giải:

+ Trường hợp 1. Nếu cos x = 0 ⇒ sin² x= 1

Thay vào phương trình đã cho ta thấy không thỏa mãn

+ Trường hợp 2. Nếu cosx ≠ 0.

Chia cả hai vế cho cos² x ta được:

4tan² x + 5tanx – 9=0

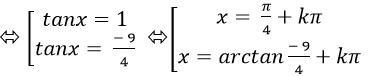
Chọn A.

Câu 2:Giải phương trình – sin² x – 2sin2x- 4cos² x = 0

A. x = arctan (-3)+ kπ

B. x = arctan 3+ kπ

C. x = arctan 2+ kπ

D. x = arctan (-2)+ kπ

Lời giải:

+ Trường hợp 1. Nếu cosx = 0 ⇒ sin² x= 1

Thay vào phương trình đã cho ta thây không thỏa mãn.

+ Trường hợp 2. Nếu cosx ≠ 0.

Ta có: - sin² x – 2sin2x – 4cos² x = 0

⇒ -sin² x – 4sinx. cosx – 4cos² x= 0

Chia cả hai vế của phương trình cho cos² x ta được :

- tan² x – 4tanx – 4= 0

⇒ - (tanx + 2)² = 0

⇒ tanx +2= 0 ⇒ tanx = - 2

⇒ x = arctan (-2)+ kπ

Chọn D

Câu 3:Giải phương trình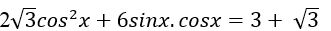

A.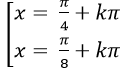

B.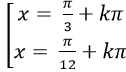

C.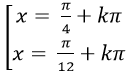

D.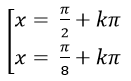

Lời giải:

Áp dụng công thức hạ bậc và công thức nhân đôi ta có:

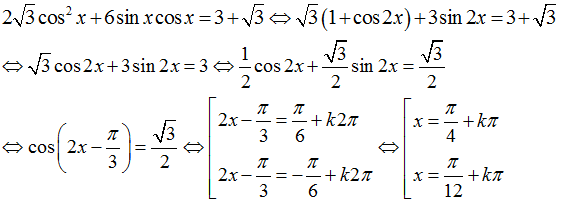
Chọn C.

Câu 4:Một họ nghiệm của phương trình: sin² x – 3sinx. cosx = 2 là

A.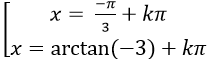

B.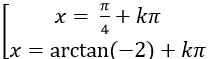

C.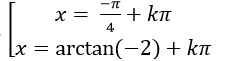

D.Đáp án khác

Lời giải:

+ Trường hợp 1. Nếu cosx= 0 ⇒ sin²x= 1 thay vào phương trình đã cho thấy không thỏa mãn.

+ Trường hợp 2. Nếu cosx ≠ 0; chia cả hai vế phương trình cho cos² x ta được :

tan² x – 3tanx = 2/(cos² x)

⇒ tan² x -3tanx= 2( 1+tan² x)

⇒ tan² x – 3tanx = 2+ 2 tan² x

⇒ - tan² x – 3tanx – 2 = 0

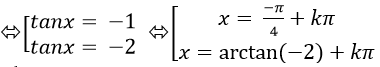
Chọn C.

Câu 5:Giải phương trình 3sin² x – 4sinx.cosx + 5cos² x = 2.

A.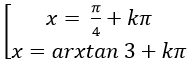

B.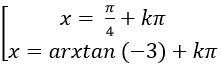

C.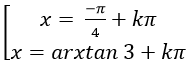

D.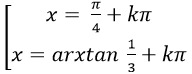

Lời giải:

+ trường hợp 1.Nếu cosx=0 ⇒ sin²x= 1 thay vào phương trình đã cho ta thấy không thỏa mãn.

+ Trường hợp 2. Nếu cosx ≠ 0.

Chia cả hai vế của phương trình cho cos² x ta được :

3tan² x – 4tan x+ 5= 2/(cos² x)

⇒ 3. tan² x – 4tanx + 5= 2( 1+ tan² x)

⇒ tan² x - 4tanx + 3= 0

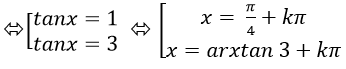
Chọn A

Câu 6:Phương trình : 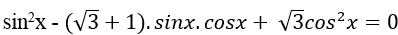có nghiệm là

A.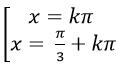

B.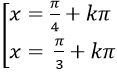

C.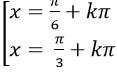

D.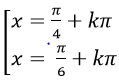

Lời giải:

+ Trương hợp 1.

Nếu cosx = 0 ⇒ sin² x= 1

Thay vào phương trình đã cho ta thấy không thỏa mãn.

+ Trường hợp 2.

Nếu cosx ≠ 0. Chia cả hai vế phương trình cho cos²x ta được :

Chọn B.

Câu 7:Phương trình 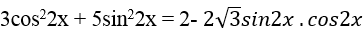có nghiệm là

A.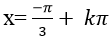

B.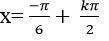

C.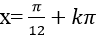

D.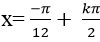

Lời giải:

+ Trường hợp 1. Nếu cos2x = 0 ⇒ sin² 2x= 1

Thay vào phương trình đã cho ta thấy không thỏa mãn.

+ Trường hợp 2.Nếu cos2x ≠ 0. Chia cả hai vế phương trình cho cos² 2x ta được :

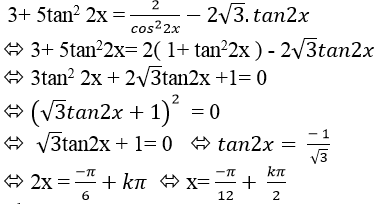
Chọn D

Câu 8:Phương trình 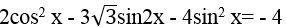có một họ nghiệm là

A.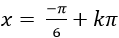

B.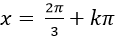

C.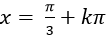

D.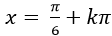

Lời giải:

+ Trường hợp 1. Nếu cosx = 0 ⇒ sin² x= 1

Thay vào phương trình đã cho ta thấy thỏa mãn.

⇒ x= π/2+kπ là nghiệm của phương trình đã cho

+ Trường hợp 2. Nếu cosx ≠ 0

Chọn D.

Câu 9:Giải phương trình sin²x + 3tanx = cosx.( 4sinx – cosx)

A.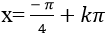

B.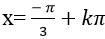

C.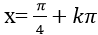

D. Đáp án khác

Lời giải:

Điều kiện : cosx ≠ 0

Ta có: sin² x+ 3tanx =cosx. (4sinx-cosx)

⇒ sin² x+ 3tanx= 4sinx. cosx- cos²x

Chia cả hai vế cho cos² x ta được :

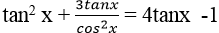
⇒ tan² x+ 3tanx (1+ tan² x)- 4tanx + 1= 0

⇒ tan² x + 3tanx + 3tan³ x – 4tanx + 1 = 0

⇒ 3tan³ x + tan² x – tanx +1= 0

⇒ tanx= - 1

⇒ x= (- π)/4+kπ

Chọn A.

Câu 10:Giải phương trình: sin² x. ( tanx+ 1) = 3sinx.(cosx – sinx) + 3

A.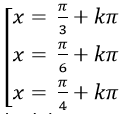

B.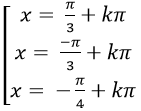

C.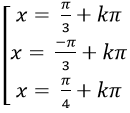

D. Đáp án khác

Lời giải:

Điều kiện: cosx ≠ 0 .

Ta có: sin² x. (tanx+ 1) = 3sinx.( cosx- sinx) + 3

⇒ sin² x. (tanx+ 1) = 3sinx. cosx – 3sin² x+ 3

⇒ sin² x.(tanx+ 1) = 3sinx.cosx + 3cos² x ( vì 3-3sin² x= 3cos² x)

Chia cả hai vế phương trình cho cos² x ≠ 0 ta được :

tan²x. ( tanx+ 1) = 3tanx + 3

⇒ tan² x. ( tanx+ 1) – (3tanx+ 3)= 0

⇒ tan² x. (tanx +1)- 3( tanx+ 1) = 0

⇒ (tan² x- 3)( tanx+ 1) = 0

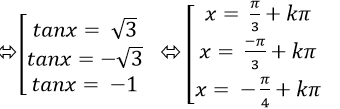
Chọn B.