Số đo của góc lượng giác và hệ thức Chasles lớp 11 (bài tập + lời giải)

---

Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Số đo của góc lượng giác và hệ thức Chasles lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Số đo của góc lượng giác và hệ thức Chasles.

Số đo của góc lượng giác và hệ thức Chasles lớp 11 (bài tập + lời giải)

1. Phương pháp giải

1.1. Cách xác định góc lượng giác

Khi xác định số đo của góc lượng giác, ta cần chú ý đến chiều quay (chiều dương: ngược chiều quay của kim đồng hồ, chiều âm: cùng chiều quay của kim đồng hồ). Từ đó xác định chính xác số đo của góc lượng giác (Ou, Ov).

Ví dụ:

– Khi đó nếu tia Om quay theo chiều dương đúng một vòng ta nói tia Om quay góc 360°, quay đúng 2 vòng ta nói nó quay 720°.

– Tia Om quay theo chiều âm nửa vòng thì ta nói nó quay góc –180°, quay theo chiều âm 1,5 vòng ta nói nó quay góc –1,5 ∙ 360° = – 540°.

Nhận xét:

+ Nếu một góc lượng giác có số đo là α° thì mọi góc lượng giác có cùng tia đầu và tia cuối với góc lượng gác đó có số đo dạng: α° + k360° (k ∈ ℤ).

+ Nếu một góc lượng giác có số đo là α rađian thì mọi góc lượng giác có cùng tia đầu và tia cuối với góc lượng gác đó có số đo dạng: α + k2π (k ∈ ℤ).

Chú ý:Cho hai tia Ou, Ov thì có vô số góc lượng giác tia đầu Ou, tia cuối Ov. Mỗi góc lượng giác như thế đều kí hiệu là (Ou, Ov). Số đo của các góc lượng giác này sai khác nhau một bội số nguyên của 360°.

1.2. Hệ thức Chasles

Với ba tia Ou, Ov, Ow bất kì, ta có:

sđ (Ou, Ov) + sđ (Ov, Ow) = sđ (Ou, Ow) + k360° (k ∈ ℤ).

2. Ví dụ minh họa

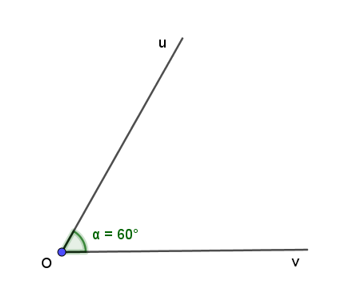
Ví dụ 1. Cho góc hình học uOv có số đo góc 60°. Xác định số đo của các góc lượng giác (Ou, Ov) và (Ov, Ou).

Hướng dẫn giải

– Các góc lượng giác có tia đầu Ou, tia cuối Ov có số đo là

sđ (Ou, Ov) = 60° + k360° (k ∈ ℤ).

– Các góc lượng giác có tia đầu Ov, tia cuối Ou có số đo là

sđ (Ov, Ou) = – 60° + k360° (k ∈ ℤ).

Ví dụ 2. Cho một góc lượng giác (Ox, Ou) có số đo 175° và một góc lượng giác (Ox, Ov) có số đo là 125°. Tính số đo của các góc lượng giác (Ou, Ov).

Hướng dẫn giải

Số đo của các góc lượng giác tia đầu Ou, tia cuối Ov là:

sđ (Ou, Ov) = sđ (Ox, Ov) – sđ (Ox, Ou) + k360°

= 125°– 175° + k360° = – 50° + k360°

= 310° – 360° + k360° = 310° + (k – 1)360°

= 310° + m360° (m = k – 1, m ∈ ℤ, k ∈ ℤ).

Vậy các góc lượng giác (Ou, Ov) có số đo là 310° + m360° (m ∈ℤ).

3. Bài tập tự luyện

Bài 1. Công thức biểu thị số đo của các góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác có số đo bằng 120° là

A. –120° + k360° (k ∈ ℤ);

B. 120° + k360° (k ∈ ℤ);

C. 120° + k180° (k ∈ ℤ);

D. –120° + k180° (k ∈ ℤ).

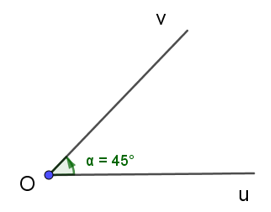
Bài 2. Cho góc hình học uOv = 45°. Xác định số đo của góc lượng giác (Ou, Ov) trong hình vẽ sau:

A. 60°;

B. – 45°;

C. 45°;

D. – 60°.

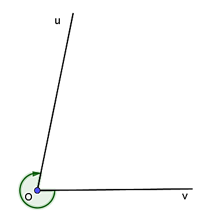
Bài 3. Cho góc hình học uOv = 75°. Xác định số đo của góc lượng giác (Ou, Ov) trong hình vẽ sau:

A. 315°;

B. –315°;

C. 285°;

D. –285°.

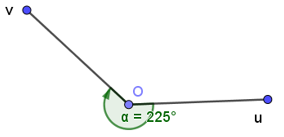
Bài 4. Xác định số đo của góc lượng giác (Ou, Ov) trong hình vẽ sau:

A. 225°;

B. –225°;

C. 135°;

D. –135°.

Bài 5. Cho góc lượng giác (OA, OB) có số đo bằng $\frac{\pi }{5}$. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác (OA, OB)?

A. $\frac{6\pi }{5}$;

B. $\frac{-11\pi }{5}$;

C. $\frac{9\pi }{5}$;

D. $\frac{31\pi }{5}.$

Bài 6. Cho góc lượng giác (OA, OB) có số đo 395°. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác (OA, OB)?

A. 45°;

B. –35°;

C. 35°;

D. –45°.

Bài 7. Trong khoảng thời gian từ 0 giờ đến 2 giờ 30 phút, kim phút quét một góc lượng giác bằng

A. – 900°;

B. – 1 000°;

C. 900°;

D. – 1 000°.

Bài 8. Các góc lượng giác (Ox, Ou) và (Ox, Ov) có số đo lần lượt là –270° và 135°. Số đo của góc lượng giác (Ou, Ov) là

A. 50° + m360°, m ∈ ℤ;

B. 45° + m360°, m ∈ ℤ;

C. –45° + m360°, m ∈ ℤ;

D. –50° + m360°, m ∈ ℤ.

Bài 9. Cho góc lượng giác (Ou, Ov) có số đo là $\frac{3\pi }{4}$, góc lượng giác (Ou, Ow) có số đo là $\frac{5\pi }{4}$. Số đo của góc lượng giác (Ov, Ow) là

A. $\frac{-\pi }{2}$+ k2π (k ∈ ℤ);

B. $\frac{\pi }{2}$+ k2π (k ∈ ℤ);

C. $\frac{-\pi }{3}$+ k2π (k ∈ ℤ);

D. $\frac{\pi }{3}$+ k2π (k ∈ ℤ).

Bài 10. Cho góc lượng giác (Ou, Ov) có số đo là $\frac{-5\pi }{4}$, góc lượng giác (Ou, Ow) có số đo là $\frac{15\pi }{4}$. Tìm số đo của góc lượng giác (Ov, Ow) biết rằng 4π < sđ (Ov, Ow) < 6π.

A. 4π;

B. 7π;

C. 5π;

D. 6π.