Tìm ảnh của một đường thẳng qua phép đối xứng trục cực hay - Toán lớp 11

Tìm ảnh của một đường thẳng qua phép đối xứng trục cực hay

Với Tìm ảnh của một đường thẳng qua phép đối xứng trục cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm ảnh của một đường thẳng qua phép đối xứng trục từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

Cách 1. Sử dụng tính chất của phép đối xứng trục

Cách 2. Sử dụng biểu thức tọa độ đối với phép đối xứng qua trục Ox hoặc Oy

B. Ví dụ minh họa

Ví dụ 1: Trong mặt phẳng tọa độ Oxy cho đường thẳng d: x + y - 3 = 0. Tìm ảnh của đường thẳng d qua phép đối xứng trục Ox.

Hướng dẫn giải:

Trục Ox có phương trình y = 0.

• Tọa độ giao điểm A của d và Ox là nghiệm của hệ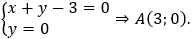

• Vì A ∈ Ox nên qua phép đối xứng trục Ox biến thành chính nó, tức A'≡A(3;0).

Chọn điểm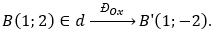

• Gọi đường thẳng d' là ảnh của d qua phép đối xứng trục Ox khi đó d’ đi qua hai điểm A'(3;0) và B'(1;-2)

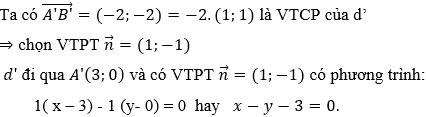
Ví dụ 2: Trong mặt phẳng tọa độ Oxy cho đường thẳng Δ có phương trình 7x + y - 3 = 0. Tìm ảnh của Δ qua phép đối xứng trục Oy.

Hướng dẫn giải:

(Sử dụng biểu thức tọa độ)

Biểu thức tọa độ qua phép đối xứng trục tung là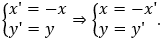

Thay vào Δ, ta được 7(-x') + y' - 3 = 0 hay 7x' - y' + 3 = 0.

Vậy ảnh của Δlà: Δ': 7x - y + 3 = 0

Ví dụ 3: Cho đường thẳng (d) có phương trình x + y-7 = 0 và đường thẳng (Δ) có phương trình 2x - y - 2 = 0. Phương trình đường thẳng (d') là ảnh của đường thẳng (d) qua phép đối xứng trục (Δ) là

Hướng dẫn giải:

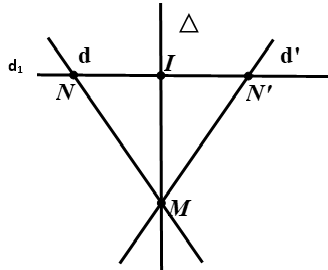
• Gọi M = (d)∩(Δ) khi đó tọa độ của M là nghiệm của hệ: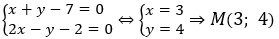

Lấy N(1;6) ∈ (d).

• Gọi (d₁) là đường thẳng qua N và vuông góc với (Δ), khi đó: (d₁): x + 2y + c = 0

N(1;6) ∈ (d₁) ⇒ 1 + 2.6 + c = 0 ⇒ c = -13 ⇒ (d₁): x + 2y - 13 = 0

• Gọi I = (d₁)∩(Δ) khi đó tọa độ của I là nghiệm của hệ: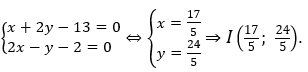

• Gọi N' là ảnh của N qua phép đối xứng trục (Δ) ⇒ I là trung điểm của NN' nên suy ra: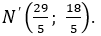

• (d') là ảnh của đường thẳng (d) qua phép đối xứng trục (Δ)

C. Bài tập trắc nghiệm

Câu 1. Trong mặt phẳng tọa độ Oxy cho đường thẳng d: x + y - 2 = 0. Ảnh của đường thẳng d qua phép đối xứng trục Ox có phương trình là:

A. x - y - 2 = 0.

B. x + y + 2 = 0.

C. -x + y - 2 = 0.

D. x - y + 2 = 0.

Lời giải:

.

Cách 1. Trục Ox có phương trình y = 0.

Tọa độ giao điểm A của d và Ox thỏa mãn hệ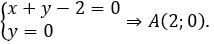

Vì A ∈ Ox nên qua phép đối xứng trục Ox biến thành chính nó, tức A'≡A(2;0).

Chọn điểm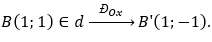

Vậy đường thẳng d' là ảnh của d qua phép đối xứng trục Ox đi qua hai điểm A'(2;0) và B'(1;-1) nên có phương trình x - y - 2 = 0.

Chọn A.

Cách 2. Biểu thức tọa độ qua phép đối xứng trục Ox là 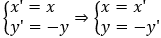. Thay vào d, ta được x' - y' - 2 = 0.

Câu 2. Trong mặt phẳng tọa độ Oxy cho đường thẳng Δ có phương trình 5x + y - 3 = 0. Đường thẳng đối xứng của Δ qua trục tung có phương trình là:

A. 5x + y + 3 = 0.

B. 5x - y + 3 = 0.

C. x + 5y + 3 = 0.

D. x - 5y + 3 = 0.

Lời giải:

.

Biểu thức tọa độ qua phép đối xứng trục tung là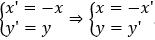

Thay vào Δ, ta được -5x' + y' - 3 = 0 hay 5x' - y' + 3 = 0.

Chọn B.

Câu 3. Trong mặt phẳng tọa độ Oxy, gọi a là đường phân giác của góc phần tư thứ nhất. Ta xét đường thẳng Δ:3x - 4y + 5 = 0. Phép đối xứng trục Đ_a biến đường thẳng Δ thành đường thẳng Δ' có phương trình là:

A. 4x - 3y - 5 = 0.

B. 3x + 4y - 5 = 0.

C. 4x - 3y + 5 = 0.

D. 3x + 4y + 5 = 0.

Lời giải:

.

• Với mỗi điểm M(x,y) ∈ Δ có tương ứng một điểm M'(x',y') ∈ Δ'

• Biểu thức tọa độ qua phép đối xứng Đ_a là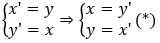

• Thay (*) vào phương trình của đường thẳng Δ, ta được 3y' - 4x' + 5 = 0 ⇔ 4x' - 3y' - 5 = 0. Suy ra Δ': 4x - 3y - 5 = 0.

Chọn A

Câu 4. Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình 3x + y - 1 = 0. Qua phép đối xứng trục Δ: 2x - y + 1 = 0, đường thẳng d biến thành đường thẳng d' có phương trình là:

A. 3x - y + 1 = 0.

B. x + 3y - 3 = 0.

C. x - 3y + 3 = 0.

D. x + 3y + 1 = 0.

Lời giải:

.

Tọa độ giao điểm A của d và Δ thỏa mãn hệ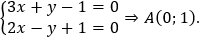

Vì A ∈ Δ nên qua phép đối xứng trục Δ biến thành chính nó, tức A' ≡ A(0;1).

Chọn điểm B(1;-2) ∈ d.

Đường thẳng đi qua điểm B và vuông góc với Δ có phương trình l: x + 2y + 3 = 0.

Gọi H = Δ ∩ l, suy ra tọa độ điểm H thỏa hệ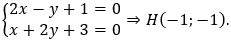

Gọi B'(x';y') là điểm đối xứng của B qua Δ → H là trung điểm của BB'

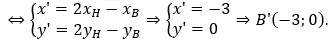
Đường thẳng d' cần tìm đi qua hai điểm A', B' nên có phương trình x - 3y + 3 = 0.

Chọn C.

Câu 5. Trong mặt phẳng tọa độ Oxy cho đường thẳng Δ: 3x - 5y + 9 = 0, phép đối xứng trục Ox biến đường thẳng Δ thành đường thẳng Δ' có phương trình là

A. -3x + 5y - 9 = 0.

B. 3x + 5y - 9 = 0.

C. 3x + 5y + 9 = 0.

D. -3x + 5y + 9 = 0.

Lời giải:

Chọn C

Giả sử M(x;y) là điểm bất kì thuộc Δ, M'(x';y') = D_Ox(M).

Biểu thức tọa độ của phép đối xứng trục Ox là: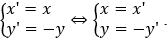

Do đó M(x';-y'), vì M ∈ Δ nên: 3x' - 5(-y') + 9 = 0 ⇔ 3x' + 5y' + 9 = 0(*)

Vì tọa độ điểm M'(x';y') thỏa mãn phương trình (*), mà khi M thay đổi thì M'chạy trên đường thẳng Δ' là ảnh của đưởng thẳng Δ qua phép đối xứng trục Ox, do đó phương trình đường thẳng Δ' là 3x + 5y + 9 = 0.

Câu 6. Trong mặt phẳng Oxy cho đường thẳng d: x + 2y + 4 = 0. Tìm ảnh của dqua phép đối xứng trục Ox.

A. d': 2x - 2y + 4 = 0.

B. d': x - 2y + 2 = 0.

C. d': 3x - 2y + 4 = 0.

D. d': x - 2y + 4 = 0.

Lời giải:

Chọn D

Tìm ảnh của d.

Lấy M(x;y) ∈ d ⇒ x + 2y + 4 = 0

Gọi N(x';y') là ảnh của M qua phép đối xứng Đ_Ox.

Ta có 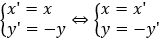. Thay vào (1) ta được

x' - 2y' + 4 = 0. Vậy d': x - 2y + 4 = 0.

Câu 7. Cho đường thẳng (d) có phương trình 4x + 3y - 5 = 0 và đường thẳng (Δ) có phương trình x + 2y - 5 = 0. Phương trình đường thẳng (d') là ảnh của đường thẳng (d) qua phép đối xứng trục (Δ) là

A. x - 3 = 0.

B. 3x + y - 1 = 0.

C. 3x + 2y - 5 = 0.

D. y - 3 = 0.

Lời giải:

Chọn D

Gọi M = (d)∩(Δ) ⇒ M(-1; 3).

Lấy N(2;-1) ∈ (d).

Gọi (d₁) là đường thẳng qua N và vuông góc với (Δ), ta có (d₁): 2x - y - 5 = 0

Gọi I = (d₁)∩(Δ) ⇒ I(3; 1).

Gọi N' là ảnh của N qua phép đối xứng trục (Δ) ⇒ I là trung điểm của NN' nên N'(4; 3).

(d') là ảnh của đường thẳng (d) qua phép đối xứng trục (Δ)

⇒ (d') là đường thẳng qua M(-1; 3) và N'(4; 3).

Vậy (d'): y - 3 = 0.

Câu 8. Cho hai đường thẳng d: x + y - 2 = 0, d₁: x + 2y - 3 = 0. Tìm ảnh của d₁ qua phép đối xứng trục d.

A. d₁': x + y - 3 = 0.

B. d₁': 2x + 2y - 3 = 0.

C. d₁': 2x + 2y - 1 = 0.

D. d₁': 2x + y - 3 = 0.

Lời giải:

.

Ta có d₁ ∩ d = I(1;1) nên Đ_d(I) = I.

Lấy M(3;0) ∈ d₁. Đường thẳng d₂ đi qua M vuông góc với d có phương trình x - y - 3 = 0. Gọi M₀ = d ∩ d₂, thì tọa độ của M₀ là nghiệm của hệ

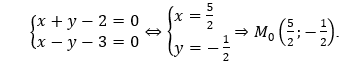
Gọi M'là ảnh của M qua Đ_d thì M₀ là trung điểm của MM'nên

M'(2;-1). Gọi d₁'= Đ_d(d₁) thì d₁' đi qua I và M'nên có phương trình

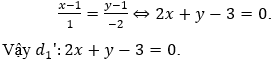
Câu 9. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x - y - 2 = 0. Ảnh của d qua phép đối xứng trục tung có phương trình:

A. x - y + 2 = 0.

B. x + y + 2 = 0.

C. x + y - 2 = 0.

D. x + 2y-2 = 0.

Lời giải:

:

Chọn B.

Lấy M(x;y) ⇒ M'(-x;y) đối xứng với M qua Oy.

Vậy ảnh của d qua phép đối xứng trục tung là:

-x - y - 2 = 0 ⇒ x + y + 2 = 0

Câu 10. Cho hai đường thẳng cắt nhau d và d'. Có bao nhiêu phép đối xứng trục biến d thành d'?

A. 0.

B. 1.

C. 2.

D. Vô số.

Lời giải:

.

Hai đường thẳng cắt nhau tạo ra 4 góc (2 cặp góc đối đỉnh bằng nhau).

Đường phân giác của 2 cặp góc đối đỉnh chính là 2 trục đối xứng biến d thành d'.

Chọn C.