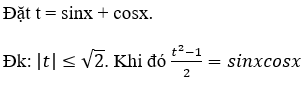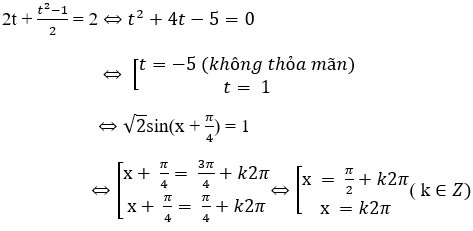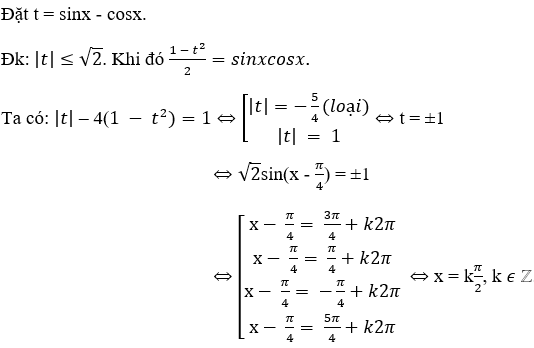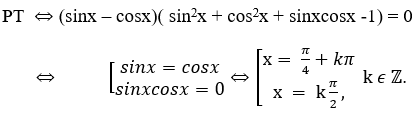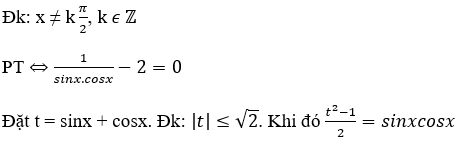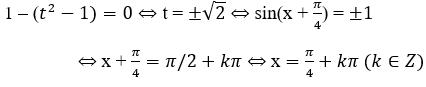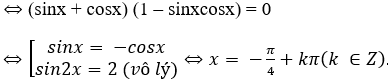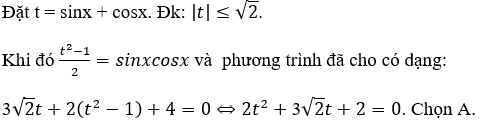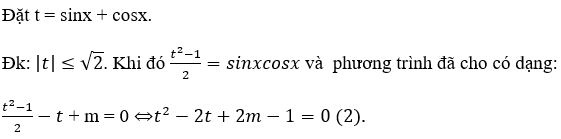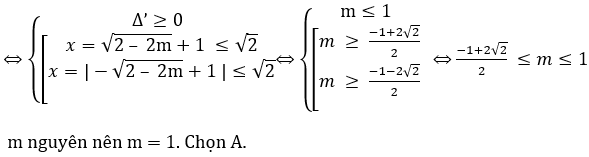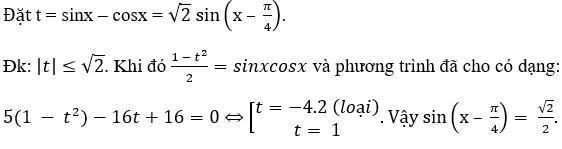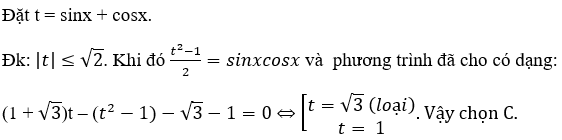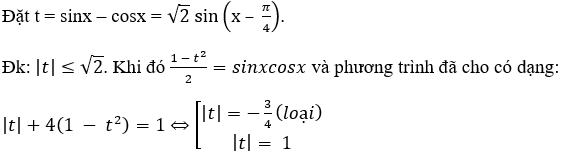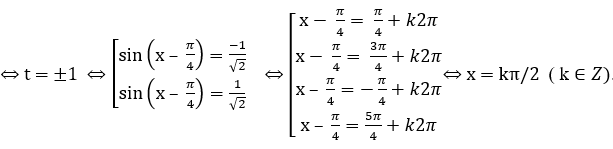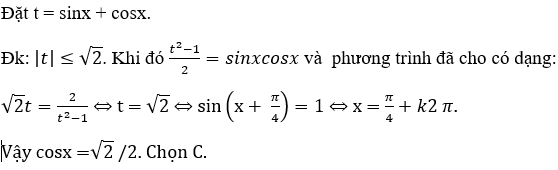Bài tập trắc nghiệm Giải phương trình lượng giác đối xứng, phản đối xứng cực hay - Toán lớp 11

---

Bài tập trắc nghiệm Giải phương trình lượng giác đối xứng, phản đối xứng cực hay

Với Bài tập trắc nghiệm Giải phương trình lượng giác đối xứng, phản đối xứng cực hay Toán lớp 11 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Giải phương trình lượng giác đối xứng, phản đối xứng từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

Bài 1: Nghiệm của phương trình 2(sinx + cosx) + sinxcosx = 2 là:

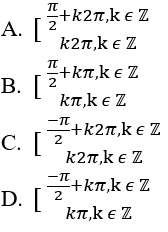
Lời giải:

Đáp án: A

Ta có phương trình đã cho có dạng:

Bài 2: Nghiệm của phương trình |sinx-cosx| + 8sinxcosx = 1 là:

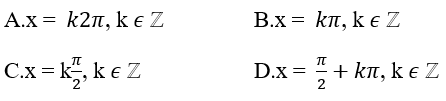
Lời giải:

Đáp án: C

Bài 3: Một nghiệm của phương trình sin³x - cos³x = sinx –cosx là:

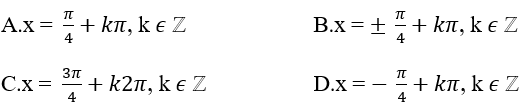
Lời giải:

Đáp án: A

Bài 4: Tập nghiệm của phương trình tanx + cotx -2 = 0 là:

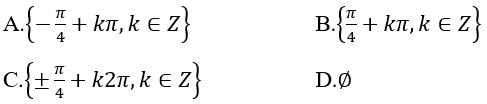
Lời giải:

Đáp án: B

Ta có phương trình đã cho có dạng:

Bài 5: Tập nghiệm của phương trình cos³x + sin³x = sinx + cosx là:

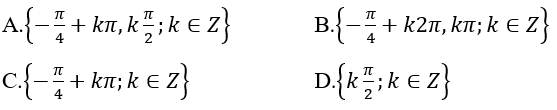
Lời giải:

Đáp án: B

cos³x + sin³x = sinx + cosx ⇔ (sinx + cosx) (1 – sinxcosx) = 0

Bài 6: Cho phương trình 3√2 (sinx+cosx)+2sin2x+4=0. Đặt t = sinx + cosx, ta được phương trình nào dưới đây?

A. 2t² + 3√2 t+2 = 0        B. 4t² + 3√2 t +4 = 0

C. 2t² + 3√2 t-2 = 0        D. 4t² + 3√2 t- 4 = 0

Lời giải:

Đáp án: A

Bài 7: Cho phương trình 5sin2x + sinx + cosx + 6 = 0. Trong các phương trình sau, phương trình nào không tương đương với phương trình đã cho?

Lời giải:

Đáp án: D

Bài 8: Nghiệm âm lớn nhất của phương trình sinx + cosx = 1 – 0.5sin2x là:

A. - 0.5π        B. – π        C. – 1.5π        D. – 2π

Lời giải:

Đáp án: C

Bài 9: Có bao nhiêu giá trị nguyên của tham số m để phương trình sinxcosx – sinx – cosx + m = 0 có nghiệm?

A.1        B. 2        C. 3        D.4

Lời giải:

Đáp án: A

Ta có ∆’ = 2 – 2m.

Để phương trình đã cho có nghiệm thì phương trình (2) phải có nghiệm và trị tuyệt đối của nghiệm nhỏ hơn √2

Bài 10: Từ phương trình 5sin2x – 16(sinx – cosx) + 16 = 0, ta tìm được sin(x - π/4) có giá trị bằng:

A. √2/2        B. -√2/2        C. 1        D. ± √2/2

Lời giải:

Đáp án: A

Bài 11: Từ phương trình (1 + √3)(cosx + sinx) – 2sinxcosx - √3-1=0, nếu ta đặt t = cosx + sinx thì giá trị của t nhận được là:

A. t = 1 hoặc t = √2.        B. t = 1 hoặc t = √3.

C. t = 1.        D. t = √3.

Lời giải:

Đáp án: C

Bài 12: Hỏi trên đoạn [0, 2018π], phương trình |sinx-cosx|+4sin2x=1 có bao nhiêu nghiệm?

A. 4037        B. 4036        C. 2018        D. 2019

Lời giải:

Đáp án: B

Từ 0 đến 2018 π có 1009 chu kì. Trong mỗi chu kì ta có 4 nghiệm vậy có 4036 nghiệm. Chọn B

Bài 13: Từ phương trình √2(sinx + cosx) = tanx + cotx, ta tìm được cosx có giá trị bằng:

A. 1        B. -√2/2        C. √2/2        D. -1

Lời giải:

Đáp án: C

Bài 14: Từ phương trình 1 + sin3x + cos3x = 3/2 . sin2x, ta tìm được cos(x + π/4) có giá trị bằng:

A. 1        B. -√2/2        C. √2/2        D. ±√2/2

Lời giải:

Đáp án: D

Bài 15: Nếu (1 + √5)(sinx-cosx)+sin2x-1-√5=0 thì sinx bằng bao nhiêu?

A. sinx = √2/2.        B. sinx = √2/2 hoặc sinx = -√2/2.

C. sinx = -1 hoặc sinx = 0.        D. sinx = 1 hoặc sinx = 0.

Lời giải:

Đáp án: D