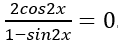Trắc nghiệm tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện - Toán lớp 11

---

Trắc nghiệm tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện

Với Trắc nghiệm tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện Toán lớp 11 tổng hợp 10 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập phương trình lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

Bài 1: Tổng các nghiệm của phương trình tan5x – tanx = 0 trên nửa khoảng [o, π) bằng:

A. π        B.2 π        C. 3π/2        D. 5 π/2.

Lời giải:

Đáp án: C

tan⁡5x = tan⁡x ⇔ x = kπ/4.x ∈ [0; π) ⇒ x = 0; π/4; π/2; 3π/4

⇒ Tổng các nghiệm: 3π/2 → Chọn C

Bài 2: Nghiệm nhỏ nhất của phương trình cosx = 1 trên [0,10 π ]là:

A. 0        B.2 π        C. 3π/2        D. 5 π/2.

Lời giải:

Đáp án: A

cos⁡x = 1 ⇔ x = k2π ⇒ nghiệm nhỏ nhất là 0 → Chọn A

Bài 3: Gọi a là nghiệm dương nhỏ nhất của phương trình sau. Mệnh đề nào sau đây đúng:

Lời giải:

Đáp án: C

ĐK sin⁡2x ≠ 1 ⇔ x ≠ π/4 + kπ

⇔ cos⁡2x = 0

⇔ 2x = π/2 + kπ

⇔ x = π/4 + kπ/2

k = 0 ⇒ x = π/4 (không thoả mãn)

k = 1 ⇒ x = 3π/4. Chọn C

Bài 4: Tập nghiệm của phương trình 2cos²5x + 3cos5x – 5 = 0 thuộc khoảng (0;π) là:

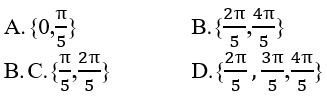
Lời giải:

Đáp án: B

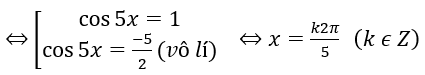
Bài 5: Trong các nghiệm của phương trình cos²xcos2x - cos² x = 0, nghiệm nằm trong khoảng (0;π) là:

A. π/2        B. 3π/2        C. π        D. 2π

Lời giải:

Đáp án: A

cos²x cos⁡2x - cos²x = 0

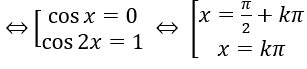
Bài 6: Tìm tất cả các giá trị thực của tham số m để phương trình cos2x – (2m + 1)cosx + m + 1 = 0 có nghiệm trên khoảng (π/2,3π/2).

A. -1 < m < 1.        B. -1 ≤ m < 0.        C. -1 < m < 0.        D. -1 < m < 0.5.

Lời giải:

Đáp án: B

cos⁡2x - (2m + 1) cos⁡x + m + 1 = 0 ⇔ 2 cos²x (2m + 1) cos⁡x + m = 0

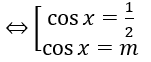
Để pt có nghiệm trên (π/2, 3π/2)thì thì cosx < 0 do đó -1 ≤ m < 0. Chọn B

Bài 7: Tính tổng T các nghiệm của phương trình cos²x – sin2x = √2 + sin²x trên khoảng (0, 2 π ).

A. T = 7 π/8        B. T = 21 π/8        C. T = 11 π/4        D. T = 3 π/4

Lời giải:

Đáp án: C

cos²x - sin⁡2x = √2 + sin²x

⇔ cos⁡2x - sin⁡2x = √2

⇔ cos⁡(2x + π/4) = 1

⇔ x = -π/8 + kπ. Trong (0, 2π).x = 7π/8; 15π/8. Chọn C

Bài 8: Số nghiệm của phương trình sin2x + √3cos2x = √3 trên khoảng (0, π/2) là?

A. 1        B. 2        C. 3        D. 4

Lời giải:

Đáp án: A

sin⁡2x + √3 cos⁡2x = √3

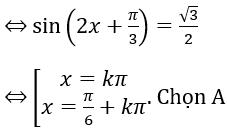
Bài 9: Số vị trí biểu diễn các nghiệm phương trình sin² x -4sinxcosx+4cos² x=5 trên đường tròn lượng giác là?

A. 4.        B.3.        C.2.        D. 1.

Lời giải:

Đáp án: C

Xét cos⁡x = 0. Pt ⇔ 1 = 5 vô lí

Xét cos⁡x ≠ 0. Chia cho cos²x . Ta được :

tan²x-4 tan⁡x + 4 = 5 tan²x + 5

⇔ 4tan²x + 4 tan⁡x + 1 = 0

⇔ tan⁡x = -1/2

⇔ x = arc tan⁡(-1/2) + kπ. Vậy có 2 điểm biểu diễn. Chọn C

Bài 10: Nghiệm dương nhỏ nhất của phương trình 4sin² x+3√3 sin2x -2cos² x=4 là:

A. π/12.        B. π/6.        C. π/4.        D. π/3.

Lời giải:

Đáp án: B

Xét cos⁡x = 0. Pt ⇔ 4 sin²x = 4

⇔ sin²x = 1

⇔ x = π/2 + kπ (k ∈ Z)

Xét cos⁡x≠0. Chia cho cos²x . Ta được :

4tan²x + 6√3 tan⁡x - 2 = 4 tan²x + 4

⇔ tan⁡x = √3/3

⇔ x = π/6 + kπ. Vậy nghiệm dương nhỏ nhất : π/6. Chọn B