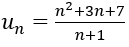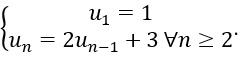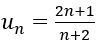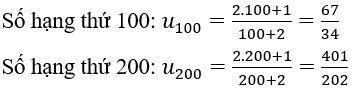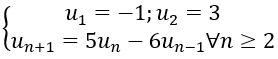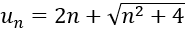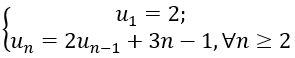Cách xác định số hạng của dãy số cực hay - Toán lớp 11

---

Cách xác định số hạng của dãy số cực hay

Với Cách xác định số hạng của dãy số cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập xác định số hạng của dãy số từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải & Ví dụ

1. Dãy số là tập hợp các giá trị của hàm số u: ¥* → i; n → u(n)

Được sắp xếp theo thứ tự tăng dần liên tiếp theo đối số tự nhiên n:

                u(1); u(2); u(3); ....u(n);....

♦ Ta kí hiệu u(n) bởi u_n và gọi là số hạng thứ n hay số hạng tổng quát của dãy số, u₁ được gọi là số hạng đầu của dãy số.

♦ Ta có thể viết dãy số dưới dạng khai triển u₁,u₂,u₃…..u_n,.... hoặc dạng rút gọn (u_n).

2. Người ta thường cho dãy số theo các cách:

♦ Cho số hạng tổng quát, tức là: cho hàm số u xác định dãy số đó

* Cho hệ thức biểu thị số hạng tổng quát qua số hạng (hoặc một vài số hạng) đứng trước nó.

Ví dụ minh họa

Bài 1: Cho dãy số có 4 số hạng đầu là: -1, 3, 19, 53. Hãy tìm một quy luật của dãy số trên và viết số hạng thứ 10 của dãy với quy luật vừa tìm.

Đáp án và hướng dẫn giải

Xét dãy (u_n) có dạng: u_n=an³+bn²+cn+d

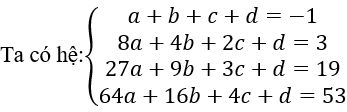
Giải hệ trên ta tìm được: a = 1 ; b = 0 ; c = -3 ; d = 1

⇒ u_n=n³-3n+1 là một quy luật .

Số hạng thứ 10: u₁₀=971.

Bài 2: Cho dãy số (u_n) được xác định bởi

1. Viết năm số hạng đầu của dãy;

2. Dãy số có bao nhiêu số hạng nhận giá trị nguyên.

Đáp án và hướng dẫn giải

Ta có năm số hạng đầu của dãy

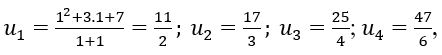
Ta có:

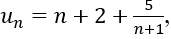
do đó u_n nguyên khi và chỉ khi 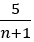nguyên hay n+1 là ước của 5. Điều đó xảy ra khi n+1=5 ⇒ n = 4

Vậy dãy số có duy nhất một số hạng nguyên là u₄=7.

Bài 3: Cho dãy số (u_n) xác định bởi:

1. Viết năm số hạng đầu của dãy;

2. Chứng minh rằng u_n=u₄;

Đáp án và hướng dẫn giải

1. Ta có 5 số hạng đầu của dãy là:

u₁=1;u₂=2u₁+3=5;u₃=2u₂+3=13;u₄=29; u₅=61.

2. Ta chứng minh bài toán bằng phương pháp quy nạp

* Với n = 1 ⇒ u₄=1 ⇒ bài toán đúng với n = 1

* Giả sử u_k=2^k+1-3 , ta chứng minh u_(k+1)=2^k+2-3

Thật vậy, theo công thức truy hồi ta có:

        u_k+1=2u_k+3=2(2^k+1-3)=2^k+2-3 (đpcm).

B. Bài tập vận dụng

Bài 1: Cho dãy số (u_n) có số hạng tổng quát

1. Viết năm số hạng đầu của dãy số.

2. Tìm số hạng thứ 100 và 200

3. Số 167/84 có thuộc dãy số đã cho hay không

4. Dãy số có bao nhiêu số hạng là số nguyên.

Lời giải:

1. Năm số hạng đầu của dãy là: u₁=1, u₂=5/4, u₃=7/5, u₄=3/2 ,u₅=11/7.

2.

3. Giả sử

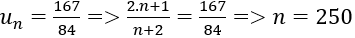
Vậy 167/84 là số hạng thứ 250 của dãy số u_n .

4. Ta có:

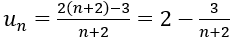
⇒ u_n nguyên khi và chỉ khi 3 chia hết cho (n+2) ⇒ n = 1

Vậy dãy số có duy nhất một số hạng là số nguyên.

Bài 2: Cho dãy số (u_n) xác định bởi:

1. Viết 7 số hạng đầu tiên của dãy

2. Chứng minh rằng: u_n=5.3^n-1-6.2^n-1∀n ≥ 1

Lời giải:

Bốn số hạng đầu của dãy

u₃=5u₂-6u₁=21; u₄=5u₃-6u₂=87; u₅=309; u₆=1023; u₇=3261 .

2. Ta chứng minh bằng phương pháp quy nạp

* u₁=5.3⁰-6.2⁰=-1(đúng)

* Giả sử u_k=5.3^(k-1)-6.2^(k-1) ∀k ≥ 2 .

Khi đó, theo công thức truy hồi ta có:

u_(k+1)=5u_k-6u_(k-1)=5.(5.3^(k-1)-6.2^(k-1) )-6(5.3^(k-2)-6.2^(k-2) )=5(5.3^(k-1)-6(3^(k-2) )-6(5.2^(k-1)-6.2^(k-2) )=5.3^k-6.2^k( đpcm).

Bài 3: Cho dãy số (u_n) có số hạng tổng quát:

1. Viết 6 số hạng đầu của dãy số

2. Tính u₂0 ,u₂010

3. Dãy số đã cho có bao nhiêu số hạng là số nguyên.

Lời giải:

1. Ta có: u₁=2+√5,u₂=4+2√2,u₃=6+√13,u₄=8+2√5,u₅=10+√29, u₆=12+2√10.

2.

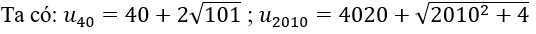
3.

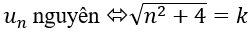
⇔ (k – n) (k + n) = 4 phương trình này vô nghiệm

Vậy không có số hạng nào của dãy nhận giá trị nguyên.

Bài 4: Cho dãy số (u_n) xác định bởi:

1. Tìm 5 số hạng đầu của dãy

2. Chứng minh rằng : u_n=5.2ⁿ-3n-5 ∀n=1,2,3…

3. Tìm số dư của u₂₀₁₀ khi chia cho 3

Lời giải:

1 Ta có: u₁=2, u₂=9, u₃=26, u₄=63, u₅=140

2. Chứng minh bằng phương pháp quy nạp

3. Ta có: 5.2²⁰¹⁰≡1.(-1)²⁰¹⁰=1(mod3)

Suy ra : u₂₀₁₀≡2(mod 3).

Bài 5: Cho dãy số (u_n):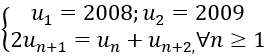

1. Chứng minh rằng dãy (v_n):v_n=u_n-u_(n-1) là dãy không đổi

2. Biểu thị u_n qua u_(n-1) và tìm CTTQ của dãy số (u_n)

Lời giải:

1. Ta có: u_(n+2)-u_(n+1)=u_(n+1)-u_n ⇒ v_(n+2)=u_(n+1)=⋯=u₂=1

2. Ta có: : u_n-u_(n-1)=1 ⇒ u_n=u_(n-1)+1

Suy ra u_n=(u_n-u_(n-1))+(u_(n-1)-u_(n-2))+⋯+(u₂-u₁)+u₁=1+1+⋯+1+u₁=n-1+2018=n+2017