Xác định tính chẵn, lẻ; tính tuần hoàn, chu kì của hàm số lớp 11 (bài tập + lời giải)

---

Haylamdo biên soan và sưu tầm trọn bộ chuyên đề phương pháp giải bài tập Xác định tính chẵn, lẻ; tính tuần hoàn, chu kì của hàm số lớp 11 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Xác định tính chẵn, lẻ; tính tuần hoàn, chu kì của hàm số.

Xác định tính chẵn, lẻ; tính tuần hoàn, chu kì của hàm số lớp 11 (bài tập + lời giải)

1. Phương pháp giải

a) Hàm số chẵn, hàm số lẻ

Để xác định tính chẵn, lẻ của hàm số y = f(x), ta thực hiện theo các bước sau:

√ Bước 1: Tìm tập xác định D của hàm số.

Tập D phải đối xứng, tức là nếu ∀x ∈ D thì –x ∈ D.

– Nếu tập D đối xứng, thực hiện tiếp Bước 2.

– Nếu tập D không đối xứng, dừng lại và kết luận hàm số không chẵn, không lẻ.

√ Bước 2: Tính f(– x) và thu gọn kết quả. Khi đó

– Nếu f(– x) = f(x): hàm số đã cho là hàm số chẵn.

– Nếu f(– x) = – f(x): hàm số đã cho là hàm số lẻ.

– Nếu không rơi vào hai trường hợp trên, ta kết luận hàm số không chẵn, không lẻ.

Chú ý:

– Các hàm số y = sin x, y = tan x, y = cot x là hàm số lẻ.

– Hàm số y = cos x là hàm số chẵn.

– Đồ thị của hàm số chẵn nhận trục tung là tung là trục đối xứng.

– Đồ thị của hàm số lẻ nhận gốc tọa độ là tâm đối xứng.

b) Hàm số tuần hoàn

Hàm số y = f(x) có tập xác định là D được gọi là hàm số tuần hoàn nếu tồn tại số T ≠ 0 sao cho với ∀x ∈ D  ta có:

i) x + T ∈ D  và x – T ∈ D;

ii) f(x + T) = f(x).

Số T dương nhỏ nhất thỏa mãn các điều kiện trên (nếu có) được gọi là chu kì của hàm số tuần hoàn đó.

→ Để xác định một hàm số là hàm số tuần hoàn, ta cần kiểm tra 2 điều kiện i) và ii).

Chú ý:

– Các hàm số y = sinx, y = cosx tuần hoàn với chu kì 2π.

– Các hàm số y = tanx, y = cotx tuần hoàn với chu kì π.

– Các hàm số y = Asin (ax + b), y = Acos (ax + b) (với a ≠ 0) tuần hoàn với chu kì $\frac{2\pi }{\left(a\right)}$.

– Các hàm số y = Atan(ax + b), y = Acot (ax + b) tuần hoàn với chu kì $\frac{\pi }{\left(a\right)}$.

– Cho cặp hàm số f(x), g(x) tuần hoàn trên tập M có chu kì lần lượt là a và b với $\frac{a}{b}\in \mathbb{Q}$. Khi đó hàm số F(x) = m.f(x) + n.g(x) tuần hoàn với chu kì T là bội chung nhỏ nhất của a và b.

2. Ví dụ minh họa

Ví dụ 1. Xét tính chẵn lẻ của các hàm số sau:

a) y = 2sinx + 3tanx;

b) y = x sin²⁰²³x ∙ cos 4x.

Hướng dẫn giải:

a) Đặt y = f(x) = 2sinx + 3tanx.

Tập xác định của hàm số là .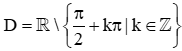

Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D.

Ta có: f(–x) = 2sin(–x) + 3tan(–x) = –2sinx – 3tanx = – (2sinx + 3tanx) = –f(x), ∀x ∈ D.

Vậy y = 2sinx + 3tanx là hàm số lẻ.

b) Đặt y = f(x) = x sin²⁰²³x ∙ cos 4x.

Tập xác định của hàm số là D = ℝ.

Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D.

Ta có: f(– x) = (– x) sin²⁰²³(– x) ∙ cos (– 4x) = x sin²⁰²³x ∙ cos 4x.

Vậy y = x sin²⁰²³x ∙ cos 4x là hàm số chẵn trên D.

Ví dụ 2. Xác định chu kì của các hàm số sau:

a) y = 4sin² 2x;

b) y = sin2x + cos4x.

Hướng dẫn giải:

a) Ta có: $y=4{\sin }^{2}2x=4.\frac{1-\cos 4x}{2}=2-2\cos 4x$.

Vậy hàm số y = 4sin² 2x tuần hoàn với chu kì $T=\frac{2\pi }{4}=\frac{\pi }{2}$.

b) Hàm số f(x) = sin2x tuần hoàn với chu kì $T_1=\frac{2\pi }{2}=\pi$.

Hàm số g(x) = cos4x tuần hoàn với chu kì $T_2=\frac{2\pi }{4}=\frac{\pi }{2}$.

Vậy hàm số y = f(x) + g(x) = sin2x + cos4x tuần hoàn với chu kì π.

3. Bài tập tự luyện 

Bài 1. Khẳng định nào dưới đây đúng?

A. Hàm số y = tan x là hàm số chẵn;

B. Hàm số y = sin x là hàm số chẵn;

C. Hàm số y = cos x là hàm số chẵn;

D. Hàm số y = cot x là hàm số chẵn.

Bài 2. Hàm số nào sau đây là hàm số chẵn?

A. y = xsinx;

B. y = xcosx;

C. y = tanx;

D. y = cotx.

Bài 3. Hàm số nào sau đây là hàm số chẵn trên ℝ?

A. y = 2x² + x;

B. $y=\frac{\text{sinx}}{x}$ ;

C. y = sin² x;

D. y = xtan2x.

Bài 4. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó?

A. $y=\sqrt{\cos x-2}$ ;

B. $y=\frac{s{\text{in}}^5\text{x}}{x}$ ;

C. y = sin2x;

D. y = |x| – x³ + 2 023.

Bài 5. Có bao nhiêu hàm số trong các hàm số y = sin2x; y = xcosx; y = |x| tan²x; y = 1 là hàm chẵn trên ℝ?

A. 1;

B. 2;

C. 3;

D. 4.

Bài 6. Cho bốn mệnh đề sau:

i) Trên ℝ, y = sin2x có tập giá trị là [–1; 1].

ii) Trên 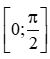, y = sinx có tập giá trị là [–1; 1].

iii) Trên ℝ, y = xsinx là hàm số chẵn.

iv) Trên ℝ, y = x sin²x là hàm số lẻ.

Số mệnh đề đúng là

A. 1;

B. 2;

C. 3;

D. 4.

Bài 7. Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A. y = x²;

B. y = sinx;

C. y = sinx + x;

D. $y=\sqrt{x}$.

Bài 8. Hàm số nào sau đây tuần hoàn với chu kì 2π?

A. y = sin2x;

B. y = cosx;

C. y = tanx;

D. y = cotx.

Bài 9. Hàm số nào sau đây không tuần hoàn với chu kì π?

A. y = sin2x;

B. y = sinx;

C. y = tanx;

D. y = cotx.

Bài 10. Hàm số y = 1 – 5cos2x tuần hoàn với chu kì là

A. 2π;

B. π;

C. 8π;

D. $\frac{\pi }{2}$.

Bài 11. Hàm số $y=\sin x+\tan \frac{x}{3}$ tuần hoàn với chu kì là

A. 2π;

B. π;

C. 8π;

D. 6π.

Bài 12. Chu kì tuần hoàn của hàm số y = 4sinxcosx + 5 là

A. 2π;

B. π;

C. 8π;

D. 6π.

Bài 13. Cặp hàm số nào sau đây có chu kì tuần hoàn khác nhau?

A. y = 2cosx và $y=\cot \frac{x}{2}$;

B. y = –3sinx và y = tan2x;

C. $y=\sin \frac{x}{2}$ và $y=\cos \frac{x}{2}$;

D. y = 2tan(2x – 10) và y = cot(2x – 10).