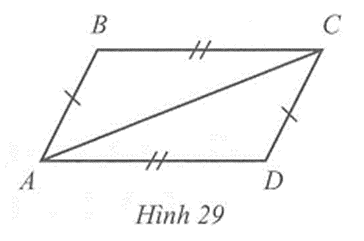
Cho Hình 29, có BC = AD, AB = CD. Chứng minh: a, tam giác ABC = tam giác CDA

Cho có BC = AD, AB = CD. Chứng minh:

Giải vở bài tập Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh

Câu 6 trang 81 vở bài tập Toán lớp 7 Tập 2:Cho Hình 29, có BC = AD, AB = CD. Chứng minh:

a) ∆ABC = ∆CDA;

b) AB // CD; AD // BC.

Lời giải:

a) Xét hai tam giác ABC và CDA, ta có:

AC là cạnh chung, AB = CD, BC = AD (giả thiết).

Suy ra ∆ABC = ∆CDA (c.c.c).

b) Ta có ∆ABC = ∆CDA nên $\widehat{\mathrm{BAC}}$= $\widehat{\text{DCA}}$ (hai góc tương ứng)

Lại có $\widehat{\mathrm{BAC}}$ , $\widehat{\text{DCA}}$ là hai góc so le trong. Suy ra AB // CD

Tương tự, ta có $\widehat{\text{ACB}}$= $\widehat{\text{CAD}}$ . Lại có $\widehat{\text{ACB}}$, $\widehat{\text{CAD}}$ là hai góc so le trong. Suy ra AD // BC.