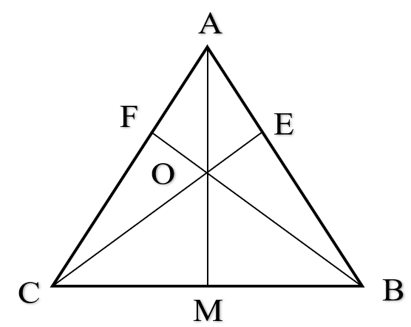
Cho tam giác ABC cân tại A. Trên AB và AC lần lượt lấy hai điểm E và F

Cho tam giác ABC cân tại A. Trên AB và AC lần lượt lấy hai điểm E và F sao cho AE = AF. Hai đoạn thẳng BF và CE cắt nhau tại O, chứng minh AO là đường trung trực của BC.

Giải vở thực hành Toán 7 Bài 10: Bài tập cuối chương 8

Bài 4 trang 65 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC cân tại A. Trên AB và AC lần lượt lấy hai điểm E và F sao cho AE = AF. Hai đoạn thẳng BF và CE cắt nhau tại O, chứng minh AO là đường trung trực của BC.

Lời giải:

Kéo dài AO cắt BC tại M.

Xét tam giác ACE và tam giác ABF.

AC = AB ( do tam giác ABC cân tại A)

AE = AF (gt)

Góc A chung

Vậy tam giác ACE bằng tam giác ABF theo trường hợp c.g.c. Suy ra CE = BF.

Xét tam giác ECB và tam giác FBC

$\widehat{\text{EBC}}=\widehat{\text{FCB}}$ ( do tam giác ABC cân tại A)

CE = BF

Cạnh chung BC

Vậy tam giác ECB bằng tam giác FBC theo trường hơpk c.g.c. Suy ra $\widehat{\text{ECB}}=\widehat{\text{FBC}}\text{}$hay $\widehat{\text{OCB}}=\widehat{\text{OBC}}\text{}$ nên tam giác OBC cân tại O. Ta có OB = OC hay O nằm trên đường trung trực của BC (1).

AB = AC ( do tam giác ABC cân tại A) nên A nằm trên đường trung trực của BC. (2)

Từ (1) và (2) suy ra AO là đường trung trực của BC.