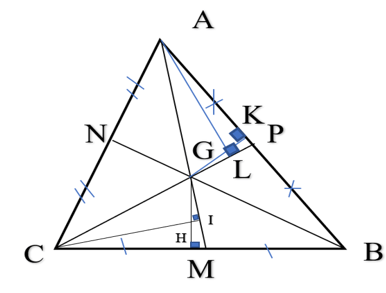
Cho tam giác nhọn ABC có AM, BN, CP là ba trung tuyến và G là trọng tâm của tam giác
Cho tam giác nhọn ABC có AM, BN, CP là ba trung tuyến và G là trọng tâm của tam giác.
Giải vở thực hành Toán 7 Bài 10: Bài tập cuối chương 8
Bài 5 trang 65 Vở thực hành Toán 7 Tập 2: Cho tam giác nhọn ABC có AM, BN, CP là ba trung tuyến và G là trọng tâm của tam giác.
a) Chứng minh 2S∆APG = 2S∆BGP = S∆AGC.
b) Chứng minh diện tích ba tam giác GAB, tam giác GBC và tam giác GAC bằng nhau.
Lời giải:
a) Từ G hạ đường vuông góc GK xuống AB.
Do PA = PB nên 2S∆APG = AP.GK = BP.GK = 2S∆BGP.
Từ A hạ đường vuông góc AL xuống CP.
Do GC = 2 GP nên 2S∆AGP = PG. AL = GC.AL = 2S∆AGC.
Vậy 2S∆APG = 2S∆BGP = S∆AGC.
b) Do 2S∆AGP = S∆ABG nên áp dụng câu a ta có:
S∆ABG= S∆AGC . (1)
Tương tự ta có:
Từ G hạ đường vuông góc GH xuống BC.
Do BC = 2 MC nên 2S∆GMC = 2GM.CM = GM.BC = S∆GBC.
Từ C hạ đường vuông góc CI xuống AM.
Do AG = 2GM nên 2S∆GMC = CI.GM = CI.AG = S∆GAC.
Vậy S∆GBC = S∆GAC. (2)
Từ (1) và (2) suy ra diện tích ba tam giác GAB, tam giác GBC và tam giác GAC bằng nhau.