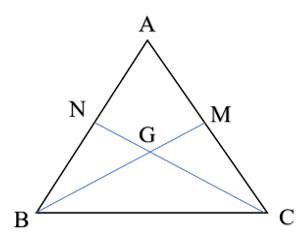
Cho tam giác ABC có hai trung tuyến BM và CN cắt nhau tại G

Cho tam giác ABC có hai trung tuyến BM và CN cắt nhau tại G. Biết BM = CN, chứng minh tam giác GBC và tam giác GMN cùng cân tại G.

Giải vở thực hành Toán 7 Bài 7: Tính chất ba đường trung tuyến của tam giác

Bài 8 trang 56 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC có hai trung tuyến BM và CN cắt nhau tại G. Biết BM = CN, chứng minh tam giác GBC và tam giác GMN cùng cân tại G.

Lời giải:

Theo định lí về ba đường trung tuyến trong tam giác ta có:

GC = $\frac{2}{3}$CN.

GB = $\frac{2}{3}$BM.

Mà BM = CN (gt) nên GB = GC. Suy ra tam giác GBC cân tại G.

GN = CN – GC = BM – GB = GM. Suy ra tam giác GMN cân tại G.