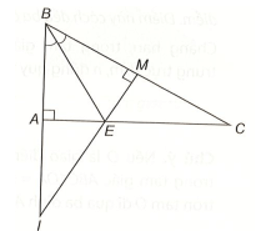
Cho tam giác ABC vuông tại A có góc B bằng 60 độ. Tia phân giác của góc ABC cắt AC ở E

Cho tam giác ABC vuông tại A có góc B bằng 60°. Tia phân giác của góc ABC cắt AC ở E. Kẻ EM vuông góc với BC (M ∈ BC).

Giải vở thực hành Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

Bài 6 trang 79 vở thực hành Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A có góc B bằng 60°. Tia phân giác của góc ABC cắt AC ở E. Kẻ EM vuông góc với BC (M ∈ BC).

a) Chứng minh ∆ABE = ∆MBE.

b) Chứng minh MB = MC.

c) Gọi I là giao điểm của BA và ME. Chứng minh IE > EM.

Lời giải:

a) Xét hai tam giác vuông ABE và MBE, ta có:

BE cạnh chụng, $\widehat{ABE}=\widehat{MBE}$ (BE là tia phân giác góc ABC).

Do đó ∆ABE = ∆MBE (cạnh huyền – góc nhọn).

b) Trong tam giác vuông ABC, ta có $\widehat{B}=60°$ nên $\widehat{C}=90°-60°=30°$.

Vì BE là tia phân giác của $\widehat{ABC}$ nên $\widehat{ABE}=\widehat{CBE}=\frac{\widehat{ABC}}{2}=\frac{60°}{2}=30°$.

Vậy tam giác BEC có $\widehat{C}=\widehat{CBE}=30°$ nên tam giác BEC cân tại E.

Tam giác BEC cân tại E và có EM là đường cao nên cũng là trung tuyến , suy ra MB = MC.

c) Ta có góc $\widehat{EAI}$ kề bù với góc vuông $\widehat{BAC}$ nên $\widehat{EAI}=90°$.

Trong tam giác vuông AEI có cạnh IE là cạnh huyền nên IE > AE.       (1)

Theo câu a) ∆ABE = ∆MBE  nên AE = EM.           (2)

Từ (1) và (2) suy ra IE > EM.