Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC
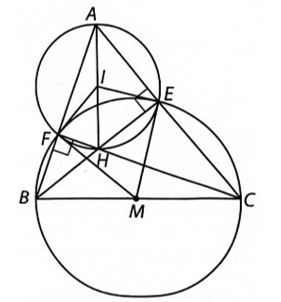
Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng:
Giải vở thực hành Toán 9 Bài tập cuối chương 9 - Kết nối tri thức
Bài 1 trang 110 VTH Toán 9 Tập 2: Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng:
a) Tứ giác AEHF nội tiếp một đường tròn tâm I;
b) ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.
Lời giải:
a) Do hai tam giác AEH và AFH vuông tại E và F nên IE = IA = IH = IF.
Vì vậy tứ giác AEHF nội tiếp đường tròn (I, IA).
b) Tương tự như trên, tứ giác BCEF có nên tứ giác BCEF nội tiếp đường tròn (M, MB).
Suy ra
Vì ∆IFA cân tại I nên (1)
Mặt khác, ta có MF = MC, hay ∆MFC cân tại M. Suy ra (2)
Vì vậy ta có:
(theo (1) và (2)).
Do đó MF ⊥ IF. Suy ra MF tiếp xúc với (I, IA). Tương tự MR tiếp xúc với (I, IA).
Lời giải vở thực hành Toán 9 Bài tập cuối chương 9 hay khác: