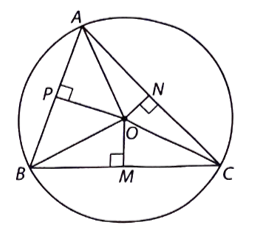
Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm
Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.
Giải vở thực hành Toán 9 Bài tập cuối chương 9 - Kết nối tri thức
Bài 2 trang 111 VTH Toán 9 Tập 2: Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.
Lời giải:
Do các tam giác AOB, AOC, BOC đều cân tại O nên OP, ON, OM lần lượt là các đường cao của các tam giác này.
Do vậy, tứ giác ANOP có
Do vậy tứ giác ANOP nội tiếp đường tròn có tâm là trung điểm của AO và bán kính bằng Tương tự BPOM, CMON cũng là các tứ giác nội tiếp.
Lời giải vở thực hành Toán 9 Bài tập cuối chương 9 hay khác: