Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C

❮ Bài trước Bài sau ❯

Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.

Giải vở thực hành Toán 9 Bài 13: Mở đầu về đường tròn - Kết nối tri thức

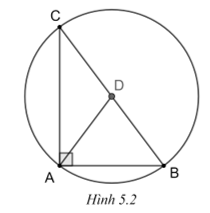
Bài 2 trang 98 VTH Toán 9 Tập 1: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.

Lời giải:

(H.5.2).

Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C

Gọi O là trung điểm của BC.

Xét tam giác ABC vuông tại A có AO là đường trung tuyến ứng với cạnh huyền BC nên $A O = O B = O C = \frac{B C}{2} .$

Do đó, ba điểm A, B, C cùng cách đều điểm O nên A, B, C cùng thuộc đường tròn tâm O, bán kính $\frac{B C}{2} .$

Áp dụng định lí Pythagore trong tam giác ABC vuông tại A, ta có:

$B C^{2} = A B^{2} + A C^{2} = 3^{2} + 4^{2} = 9 + 16 = 25,$ suy ra $B C = \sqrt{25} = 5$ (cm).

Do đó $R = \frac{B C}{2} = \frac{5}{2} = 2, 5$ (cm).

Vậy ba điểm A, B, C cùng thuộc một đường tròn tâm O bán kính 2,5 cm.

Lời giải vở thực hành Toán 9 Bài 13: Mở đầu về đường tròn hay khác:

Vở thực hành Toán 9

Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C

Giải vở thực hành Toán 9 Bài 13: Mở đầu về đường tròn - Kết nối tri thức

Xem thêm các bài giải vở thực hành Toán lớp 9 Kết nối tri thức hay, chi tiết khác: