Cho tam giác ABC cân tại A có ba đỉnh nằm trên đường tròn (O). Đường cao AH cắt (O) tại D

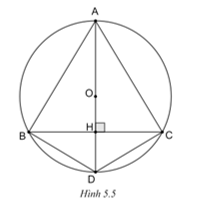
Cho tam giác ABC cân tại A có ba đỉnh nằm trên đường tròn (O). Đường cao AH cắt (O) tại D. Biết BC = 24 cm, AC = 20 cm. Tính chiều cao AH và bán kính đường tròn (O).

Giải vở thực hành Toán 9 Bài 13: Mở đầu về đường tròn - Kết nối tri thức

Bài 5 trang 100 VTH Toán 9 Tập 1: Cho tam giác ABC cân tại A có ba đỉnh nằm trên đường tròn (O). Đường cao AH cắt (O) tại D. Biết BC = 24 cm, AC = 20 cm. Tính chiều cao AH và bán kính đường tròn (O).

Lời giải:

(H.5.5)

Vì tam giác ABC cân tại A nên đường cao AH cũng là đường trung trực của đoạn BC, suy ra H là trung điểm của BC.

Tam giác ACH vuông tại H nên theo định lí Pythagore, ta được

$A{H}^2=A{C}^2-C{H}^2=A{C}^2-{\left(\frac{BC}{2}\right)}^2={20}^2-{\left(\frac{24}{2}\right)}^2=256.$

Suy ra $AH=\sqrt{256}=16$ (cm).

Tam giác ACD có AD là đường kính nên tam giác ACD là tam giác vuông tại C.

Trong tam giác ACD vuông tại C, ta có:

$A{C}^2=AH.AD,$ suy ra $AD=\frac{A{C}^2}{AH}=\frac{{20}^2}{16}=25$ (cm).

Vậy bán kính của đường tròn (O) là $R=\frac{AD}{2}=\frac{25}{2}=12,5$ (cm).

Lời giải vở thực hành Toán 9 Bài 13: Mở đầu về đường tròn hay khác:

• Câu 1 trang 97 VTH Toán 9 Tập 1: Chọn phương án đúng. Cho tam giác ABC vuông tại A. Tâm đường tròn đi qua ba đỉnh của tam giác ABC là ...

• Câu 2 trang 97 VTH Toán 9 Tập 1: Chọn phương án đúng. Trên mặt phẳng tọa độ Oxy, cho các điểm ...

• Câu 3 trang 98 VTH Toán 9 Tập 1: Chọn phương án đúng. Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H ...

• Câu 4 trang 98 VTH Toán 9 Tập 1: Chọn phương án đúng. Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn ...

• Bài 1 trang 98 VTH Toán 9 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M(0; 2), N(0; −3) và P(2; −1) ...

• Bài 2 trang 98 VTH Toán 9 Tập 1: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng ...

• Bài 3 trang 99 VTH Toán 9 Tập 1: Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d ...

• Bài 4 trang 99 VTH Toán 9 Tập 1: Cho hình vuông ABCD có E là giao điểm của hai đường chéo ...