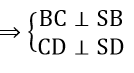Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và vuông

Bài tập ôn tập chương 3 (phần Hình học)

Bài 3 trang 121 Toán 11: Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD)

a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.

b) Mặt phẳng (α) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, SC, SD tại B’, C’, D’. Chứng minh B’D’ song song với BD và AB’ vuông góc với SB’.

Trả lời

a)Áp dụng định lí ba đường vuông góc

Suy ra SBC, SCD là những tam giác vuông

Ta cũng có SAD, SAB là những tam giác vuông

b)Ta có: ABCD là hình vuông BD ⊥ AC

SA ⊥ (ABCD) ⇒ BD ⊥ SA

Vậy BD ⊥ (SAC) ⇒ BD ⊥ SC     (1)

Ta cũng có : SC ⊥ (α) ⇒ SC ⊥ B’D’    (2)

Do B’D’ và BD cùng thuộc (SBD),

Nên từ (1) (2) suy ra B’D’ // BD

Ta có: BC ⊥ (SAB) ⇒ BC ⊥ AB’    (3)

Mặt khác SC ⊥ (α) ⇒ SC ⊥ AB’      (4)

(3)và (4) AB’ ⊥ (SBC) ⇒ AB’⊥ SB.