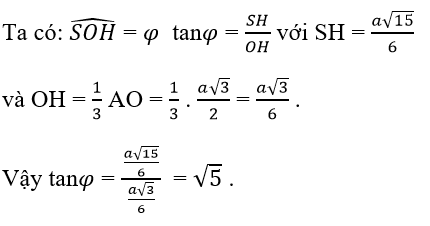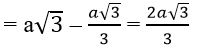Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có góc ∠BAD= 60º

Bài tập ôn tập chương 3 (phần Hình học)

Bài 7 trang 122 Toán 11: Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có góc ∠BAD= 60º và SA = SB = SD = (a√3)/2 .

a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.

b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).

c) Chứng minh SB vuông góc với BC.

d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ.

Trả lời

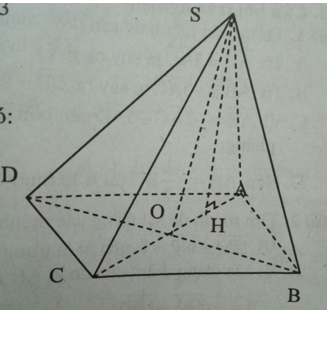
a) Kẻ SH (ABCD)

Do SA = SB = SD HA = HB = HD

Suy ra H là tâm đường tròn ngoại tiếp ΔABD.

Do AB = AD = a và ∠BAD = 60º nên ΔABD là tam giác đều cạnh a.

AO = (a√3)/2 ; AC = 2AO = a√3

Mà AH = 2/3 AO ⇒ AH = (a√3)/3

Trong tam giác vuông SAH, ta có:

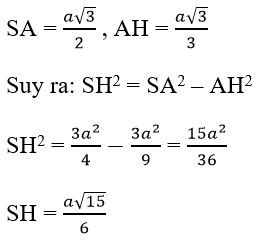
Ta cũng có: HC = AC – AH ⇒ HC

Trong tam giác vuông SHC, ta có : SC² = SH² + HC²

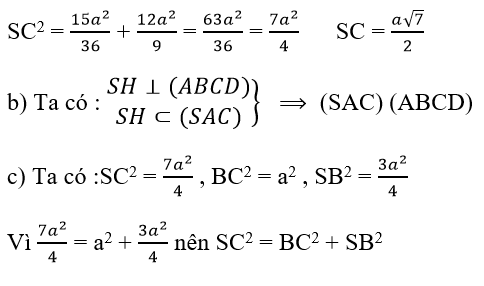
Theo định lí đảo của định lí Pitago, ta suy ra được tam giác SBC vuông tại B. Vậy SB BC.

d) Ta có: SH ⊥ (ABCD) ⇒ SH ⊥ BD và DB ⊥ AC ⇒ DB ⊥ (SAC)

Mà OS ⊂ (SAC) ⇒ DB ⊥ OS và DB ⊥ OA

⇒ ∠SOH là góc giữa hai mặt phẳng (SBD) và (ABCD).