Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có góc ∠BAD = 60º

Bài tập ôn tập chương 3 (phần Hình học)

Bài 4 trang 121 Toán 11: Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có góc ∠BAD = 60º. Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và SO = 3a/4. Gọi E là trung điểm của đoạn BC, F là trung điểm của đoạn BE.

a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC).

b) Tính các khoảng cách từ O và A đến mặt phẳng (SBC).

Trả lời

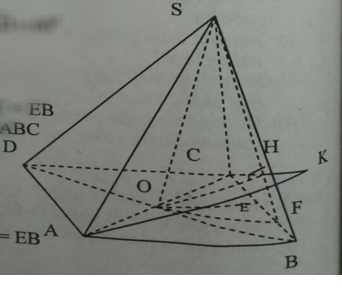
a) Ta có : ABCD là hình thoi cạnh a nên :

AB = CB = CD = DA = a

⇒ ΔABD là tam giác cân có ∠BAD = 60º.

Vậy ΔABD là tam giác đều.

⇒ BD = a OB = a/2 (1)

Mặt khác ta lại có: OA = OC và EC = EB

⇒ OE là đường trung bình của ΔABC

⇒ OE = a/2 (2)

Và EB = a/2 (3)

Từ (1), (2) và (3) suy ra OB = OE = EB.

Vậy ΔBOE là tam giác đều cạnh a/2 . Do đó OF là đường cao. Suy ra OF ⊥ BC và SO ⊥ (ABCD) ⇒ SO ⊥ BC

Mà BC ⊂ (SBC) nên suy ra (SBC) ⊥ (SOF).

b) Vì (SBC) ⊥ (SOF) và hai mặt phẳng này giao nhau theo giao tuyến SF nênnếu từ điểm O ta kẻ OH ⊥ SF thì OH ⊥ (SBC). Do đó OH chính là khoảng cách từ O đến mặt phẳng (SBC).

Ta có: SO = 3a/4 và OF² = OB² – BF²

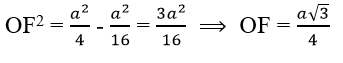
Vì SO ⊥ (ABCD) nên SO ⊥ OF ⇒ ∆SOF vuông tại O, suy ra:

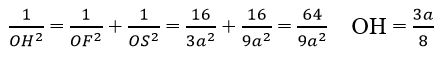
Gọi K là hình chiếu của A trên mặt phẳng (SBC), ta có AK // OH

Trong ∆AKC thì OH là đường trung bình nên suy ra AK = 2OH = 2.(3a)/8.

Vậy AK = 3a/4 .