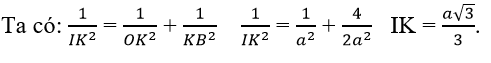Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Chứng minh BC’ vuông góc với

Bài tập ôn tập chương 3 (phần Hình học)

Bài 6 trang 122 Toán 11: Cho hình lập phương ABCD.A’B’C’D’ cạnh a.

a) Chứng minh BC’ vuông góc với mặt phẳng (A’B’CD)

b) Xác định và tính độ dài đoạn vuông góc chung của AB’ và BC’

Trả lời

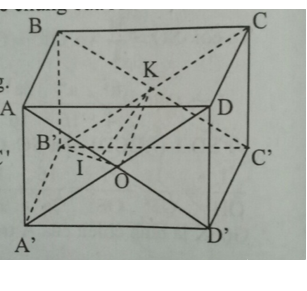
a) Vì ABCD.A’B’C’D’ là hình lập phương nên các mặt bên và mặt đáy là hình vuông.

Suy ra tứ giác BCC’B’ là hình vuông

⇒ BC’ ⊥ B’C     (1)

Ta cũng có: A’B ⊥ BB’ và A’B’ ⊥ B’C’

⇒ A’B’ ⊥ (BCC’B’) ⇒ A’B’ ⊥ BC’     (2)

Từ (1) và (2) BC’ ⊥ (A’B’CD).

b) Gọi O và K lần lượt là tâm của hai hình vuông ADD’A’ và BCC’B’. Trong mặt phẳng (A’B’CD):

Kẻ KI ⊥ B’O (I ∈ B’O)

Ta có: (AB’O) ⊥ (A’B’CD) ⇒ KI ⊥ (AOB’) ⇒ KI ⊥ AB’

Mặt khác BC’ ⊥ (A’B’CD) ⇒ BC’ ⊥ KI

Vậy KI là đường vuông góc chung của AB’ và BC’