Cho hình lập phương ABCD.A’B’C’D’ có E và F lần lượt là trung điểm của các

Bài tập ôn tập cuối năm (phần Hình học)

Bài 5 trang 126 Toán 11: Cho hình lập phương ABCD.A’B’C’D’ có E và F lần lượt là trung điểm của các cạnh AB và DD’. Hãy xác định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC’) và (EFK) với K là trung điểm của cạnh B’C’.

Trả lời

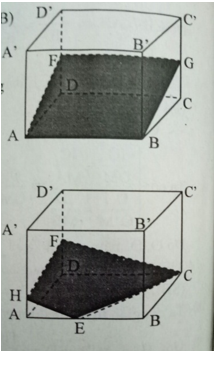
Mặt phẳng (EFB) chứa cạnh AB nên (EFB) cắt (DCC’D’) theo giao tuyến GF//AB.

Ta có thiết diện là hình chữ nhật ABGF

Thiết diện của hình hộp chữ nhật cắt bởi mặt phẳng (EFC) là CFHE với HH ∈ AA’ và EH // CF

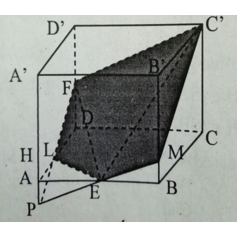
Thiết diện của hình hộp cắt bởi mặt phẳng (EFC’) là EMC’FL. Với: M ∈ BB’, L ∈ AD

EM // C’F

L = PF ∩ AD

P = EM ∩ AA’

Thiết diện của hình hộp cắt bởi mặt phẳng (EFK) là hình lục giác đều (kéo dài EK về hai phía cắt AD và DC, nối những giao điểm này với F)

HS tự vẽ hình.