Giải Toán 11 trang 126 Kết nối tri thức, Chân trời sáng tạo
Haylamdo giới thiệu lời giải bài tập Toán 11 trang 126 Kết nối tri thức, Chân trời sáng tạo sẽ giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 trang 126.
Giải Toán 11 trang 126 Kết nối tri thức, Chân trời sáng tạo
- Toán lớp 11 trang 126 Tập 1 (sách mới):
- Toán lớp 11 trang 126 Tập 2 (sách mới):
Lưu trữ: Giải Toán 11 trang 126 (sách cũ)
Bài 7 trang 126 Toán 11: Cho hình thang ABCD vuông góc tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C’, D’ lần lượt là hình chiếu vuông góc của A trên SC và SD. Chứng minh rằng:
a) ∠SBC = ∠SCD=90º
b) AD’, AC’ và AB cùng nằm trên một mặt phẳng
c) Chứng minh rằng đường thẳng C’D’ luôn luôn đi qua một điểm cố định khi S di đông trên tia Ax.
Trả lời
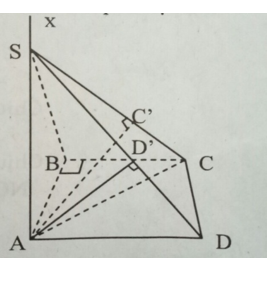
a) Ta có:
Theo định lí ba đường vuông góc
⇒ BC ⊥ SB ⇒ ∠SBC= 90º
Ta dễ dàng chứng minh được AC ⊥ CD
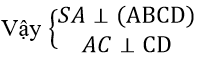
Theo định lí ba đường vuông góc SC ⊥ CD ⇒ ∠SCD = 90º
b) Theo câu a, ta có: CD ⊥ (SAC) ⇒ CD ⊥ AC’
Mặt khác: AC’ ⊥ SC ⇒ AC’ ⊥ (SCD) ⇒ AC’ ⊥ SD
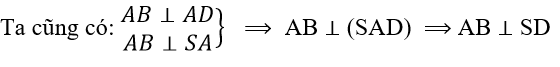
Vậy ta đã có : AB, AC’, AD’ cùng vuông góc với SD. Suy ra AB, AC’, AD’ đồng phẳng (do AB, AC’, AD’ đồng quy)
c) Theo câu b: C’D’ nằm trên giao tuyến của (ABC’D’) và (SCD).