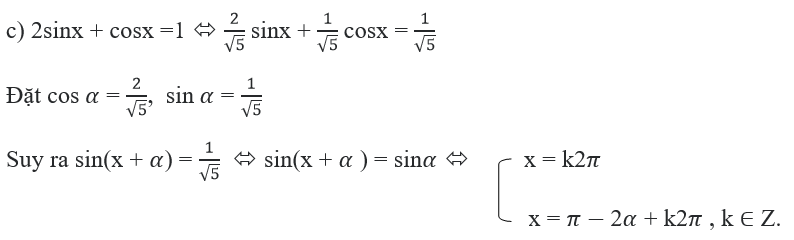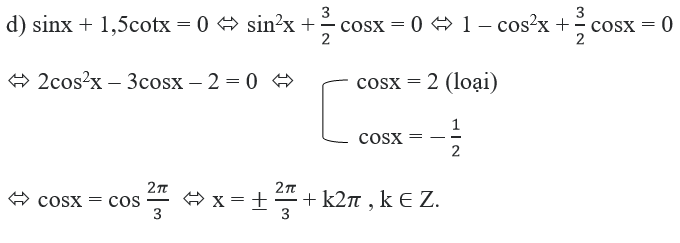Giải phương trình sau 2cos^2 x – 3cosx + 1 = 0

Ôn tập chương 1 (phần Đại số và Giải tích)

Bài 5 trang 41 Toán 11: Giải các phương trình sau:

a) 2cos²x – 3cosx + 1 = 0         b) 25sin²x + 15sin2x + 9cos²x = 15

c) 2sinx + cosx = 1;           d) sinx + 1,5cotx = 0.

Trả lời

a) 2cos²x – 3cosx + 1 = 0

Đặt t = cosx ⇒ 2t² – 3t + 1 = 0

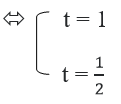
* Với t = 1 ⇒ cosx = 1 ⇔ x = k2π , k ∈ Z

* Với t = 1/2 ⇒ cosx = 1/2 ⇔ x = ± π/3 + k2π

b) 25sin²x + 15sin2x + 9cos²x = 15    (2)

Nhận thất cosx = 0 ⇔ x = π/2 + kπ là nghiệm của phương trình 25sin²x = 25 ⇔ sin²x = 1 luôn đúng.

Với cosx ≠ 0. Khi đó:

(2) ⇔ 25tan²x + 30tanx + 9 = 25(1+tan²x) ⇔ 30tanx = 16

⇔ tanx = 8/15 ⇔ x = arctan 8/15 + kπ, k ∈ Z.

Vậy phương trình có nghiệm; x = π/2 + kπ, x = arctan 8/15 + kπ, k ∈ Z.