Bài III.1, III.2, III.3, III.4, III.5 trang 54 SBT Toán 7 tập 2

Bài III.1, III.2, III.3, III.4, III.5 trang 54 SBT Toán 7 tập 2

Bài III.1: Chứng minh rằng trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ một đỉnh.

Lời giải:

Vì đường cao và đường trung tuyến xuất phát từ cùng một đỉnh lần lươt là đường vuông góc và đường xiên kẻ từ cùng một điểm đến cùng một đường thẳng nên ta có điều phải chứng minh.

Bài III.2: Cho tam giác ABC có hai đường trung tuyến AD, BE vuông góc với nhau. Chứng minh rằng BC > 2AC.

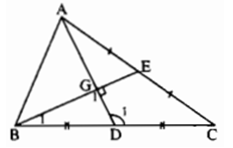
Lời giải:

BC < 2AC nếu 1/2BC = CD < AC.

Xét hai tam giác ADC có ∠D₁ = ∠G₁+ ∠B₁. Theo giả thiết ∠G₁ = 90° nên ∠D₁ là góc tù.

Cạnh AC đối diện với góc D₁ nên là cạnh lớn nhất, vậy AC > DC hay 2AC > 2DC = BC.

Bài III.3: Ba đường phân giác AD, BE, CF của tam giác ABC quy đồng tại O. Kẻ đường vuông góc OG đến BC. Chứng minh rằng ∠(BOG) = ∠(COD) .

Lời giải:

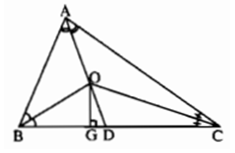
Để chứng minh ∠(BOG) = ∠(COD), ta chứng minh ∠(BOD) = ∠(GOC).

Xét tam giác OAB, ta có

∠(BOD) = 1/2(∠A + ∠B ) = 1/2 (180° − ∠C )    (1)

Xét tam giác vuông OCG ta có:

∠(GOC) = 90° − 1/2 ∠C = 1/2 ( 180° − ∠C )    (2)

Từ (1) và (2) suy ra ∠(BOD) = ∠(GOC). Vậy ∠(BOG) = ∠(COD).

Bài III.4: Cho tam giác ABC cân tại B có B = 112°. Kẻ đường cao AH và đường phân giác AD của tam giác đó. Tính các góc của tam giác AHD.

Lời giải:

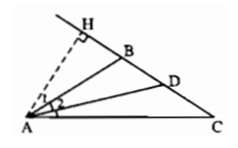
Xét tam giác vuông AHB. Ta có:

∠(ABH) = 180° − 112° = 68°

∠A₁ = 90° − ∠(ABH) = 90° − 68° = 22°

Tam giác ABC cân tại B có ∠B = 112° nên

∠(BAC) = (180° − 112°) : 2 = 34°

Do đó ∠A₂ = 34° : 2 = 17°. Từ đó

∠(HAD) = ∠A₁+ ∠A₂ = 22° + 17° = 39°.

∠(HDA) = 90° − ∠(HAD) = 90° − 39° = 51°.

Bài III.5: Cho tam giác ABC cân tại C. Kẻ các đường cao AA₁ và BB₁ của tam giác đó. Hai đường cao này cắt nhau tại M. Chứng minh rằng đường thẳng MC là đường trung trực của đoạn thẳng AB.

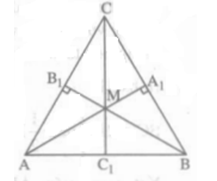
Lời giải:

Gọi giao điểm của CM và AB là C₁. Ta cần chứng minh CC₁ ⊥ AB và C₁ là trung điểm của đoạn thẳng AB. Vì trong một tam giác ba đường cao đồng quy nên CM hay CC₁ vuông góc với AB. Hai tam giác vuông CC₁A và CC₁B bằng nhau vì có ∠A = ∠B , CA = CB nên C₁ A = C₁ B hay C₁ là trung điểm của AB. Vậy MC là đường trung trực của đoạn thẳng AB.