Bài III.6, III.7, III.8 trang 55 SBT Toán 7 tập 2

Bài III.6, III.7, III.8 trang 55 SBT Toán 7 tập 2

Bài III.6: Cho tam giác ABC có ∠A = 130°. Gọi C', B'là các điểm sao cho AB là đường trung trực của CC' và AC là đường trung trực của BB'. Hai đường thẳng CB' và BC' cắt nhau tại A'. Hãy tìm bên trong tam giác A'BC điểm cách đều ba cạnh của tam giác đó.

Lời giải:

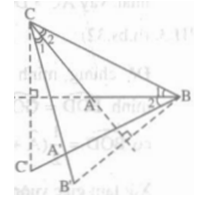
Xét tam giác A'BC. Vì AC là đường trung trực của BB' nên có ∠C₁ = ∠C₂. Vì AB là đường trung trực của CC' nên ∠B₁ = ∠B₂ Suy ra AB, AC lần lượt là đường phân giác của các góc A'BC và A'CB. Vậy ba đường phân giác của tam giác A'BC đồng quy tại A, hay A là điểm nằm trong tam giác A'BC và cách đều ba cạnh của tam giác này.

Bài III.7: Dựng các hình vuông ABDE và ACFG bên ngoài tam giác nhọn ABC cho trước.

a) Gọi H là điểm thuộc đường thẳng BC sao cho AH ⊥ BC. Gọi I, J là các điểm thuộc đường thẳng AH sao cho EI ⊥ AH và GJ ⊥ AH. Chứng minh

ΔABH = ΔEAI, ΔACH = ΔGAJ

Từ đó suy ra đường thẳng AH cắt EG tại trung điểm K của EG (tức là AK là trung tuyến của tam giác AEG)

b) Gọi L là điểm thuộc đường thẳng AK sao cho K là trung điểm của AL. Chứng minh AL = BC.

c) Chứng minh ΔABL = ΔBDC. Từ đó suy ra CD là một đường cao của tam giác BCL.

d) Chứng minh rằng các đường thẳng AH, BF, CD đồng quy.

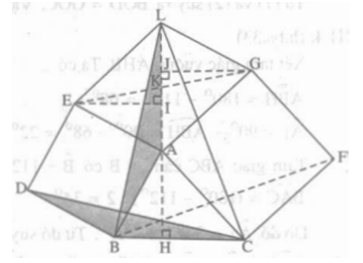
Lời giải:

a) Hai tam giác vuông ABH và EAI bằng nhau vì có AB = EA, ∠(BAH) = ∠(AEI) (cùng phụ với góc EAI). Tương tự hai tam giác vuông ACH và GAJ bằng nhau. Suy ra EI = AH = GJ. Mặt khác, ∠(JKG) = ∠(JKE) (đối đỉnh), do đó ΔEKI = ΔGKJ. Từ đó ta có trung điểm của EG. Vậy AK là trung tuyến của tam giác AEG.

b) Theo a) ΔEKI = ΔGKJ nên KI = KJ. Mặt khác, theo giả thiết K là trung điểm của Al nên AI = LJ. Ta có:

AL = AJ + JL = AJ + AI = HC + HB = BC

c) Hai tam giác ALB và BCD bằng nhau và có AL = BC, AB = BD và ∠(BAL) = 90° + ∠(EAL) = 90 + ∠(ABC) = ∠(DBC) .

Suy ra ∠(ALB) = ∠(BCD) . Mặt khác ta có ∠(ALB) + ∠(LBH) = 90° nên ∠(BCD) + ∠(LBH) = 90°.

Suy ra LB ⊥ CD, tức CD là một đường cao của tam giác LBC.

d) Lập luận tương tự câu c), ta có BF là một đường cao của tam giác LBC.

Vậy ba đường thẳng AH, BF, CD là ba đường cao của tam giác LBC nên chứng đồng quy.

Bài III.8: Cho tam giác.

a) Qua trung điểm D của cạnh BC, kẻ đường thẳng song song với AB, nó cắt cạnh AC tại E. Qua E kẻ đường thẳng song song với BC, nó cắt AB tại F. Chứng minh ΔCDE = ΔEFA. Từ đó suy ra E là trung điểm của cạnh AC.

b) Chứng minh rằng đường thẳng đi qua các trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba của tam giác đó.

c) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác ABC là trực tâm của tam giác có ba đỉnh là trung điểm ba cạnh của tam giác ABC.

Lời giải:

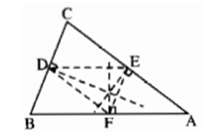
a) Ta có ΔBDF = ΔEFD (g.c.g)

Suy ra BD = EF. Theo giả thiết, D là trung điểm của BC nên CD = DB = EF.

Hai tam giác CDE và EFA bằng nhau vì CD = EF, ∠(CDE) = ∠(CBA) = ∠(EFA) và ∠(ECD) = ∠(EAF) (các góc đồng vị). Suy ra CE = EA.

b) Gọi D là trung điểm của BC, E là trung điểm của AC. Theo câu a)) đường thẳng qua D, song song với AB phải cắt AC tại trung điểm của AC nên đường thẳng đó phải đi qua E, hay DE // AB.

c) Gọi D, E, F theo thứ tự là trung điểm của BC, CA, AB. Đường trung trực của BC phải vuông góc với EF (vì (EF // BC), hay nó là một đường cao của tam giác DEF. Suy ra ba đường trung trực của tam giác ABC là ba đường cao của tam giác DEF. Do đó tâm đường tròn ngoại tiếp tam giác ABC (giao điểm của ba đường trung trực của tam giác ABC) là trực tâm của tam giác DEF.