Bài 85, 86, 87, 88, 89 trang 53 SBT Toán 7 tập 2
Bài 85, 86, 87, 88, 89 trang 53 SBT Toán 7 tập 2
Bài 85: Cho bốn điểm A, B, C, D như hình bên. Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất.
Lời giải:
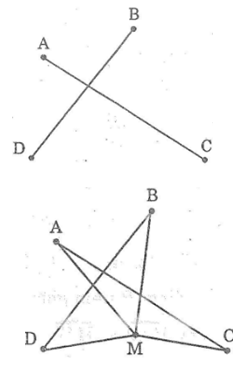
* Nếu M không trùng với giao điểm của AC và BD
Trong ΔAMC, ta có: MA + MC > AC (bất đẳng thức tam giác)
Trong ΔMBD, ta có: MB + MD > BD (bất đẳng thức tam giác)
* Nếu M trùng với giao điểm AC và BD
Ta có: MA + MC = AC
MB + MD = BD
Suy ra: MA + MC ≥ AC
MB + MD ≥ BD (dấu bằng xảy ra khi M trùng với giao điểm của AC và BD)
Suy ra: MA + MB + MC + MD ≥ AC + BD
Vậy MA + MB + MC + MD = AC + BD bé nhất khi đó M là giao điểm của AC và BD.
Bài 86: Cho hình sau trong đó G la trọng tâm của tam giác ABC. Chứng minh rằng:
a. SAGC = 2SGMC
b. SGMB = SGMC
c. SAGB = SAGC = SBGC
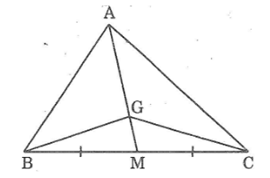
Lời giải:
a. Vì G là trung điểm của ΔABC nên GA = 2GM (tính chất đường trung tuyến)
Ta có ΔAGC và ΔGMC có chung đường cao kẻ từ đỉnh C đến AM, đồng thời cạnh đáy GA = 2GM.
Suy ra: SAGC = 2SGMC (1)
b. Ta có ΔGMB và ΔGMC có cạnh đáy MB = MC, chung đường cao kẻ từ đỉnh G đến cạnh BC
Suy ra: SGMB = SGMC (2)
c. Ta có ΔAGB và ΔGMB có chung đường cao kẻ từ đỉnh B đến cạnh AM, đồng thời AG = 2GM (chứng minh trên)
Suy ra: SAGB = 2SGMB (3)
Mà SBGC = SGMB + SGMC = 2SGMB (4)
Từ (1), (2), (3) và (4) suy ra: SAGB = SAGC = SBGC
Bài 87: Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy.
a. Hãy tìm điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy)
b. Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a?
Lời giải:
a. Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).
Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.
Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác ∠(xOy)
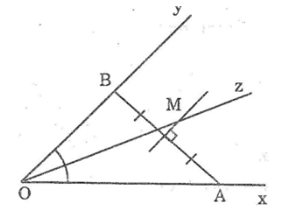
b. Nếu OA = OB thì ΔOAB cân tại O
Khi đó tia phân giác của ∠(xOy) cũng là đường trung trực của AB
Vậy bất kì điểm M nào nằm trên tia phân giác của ∠(xOy) đều thỏa mãn điều kiện trong câu a).
Bài 88: Cho góc xOy khác góc bẹt. Dùng một chiếc thước thẳng có chia khoảng, hãy nêu cách vẽ tia phân giác của góc xOy.
Lời giải:
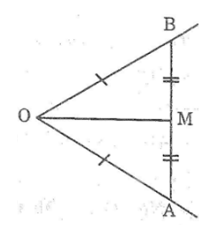
- Dùng thước chia khoảng, trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = OB.
- Nối AB.
- Dùng thước chia khoảng để đo đoạn AB, lấy trung điểm M của AB.
- Kẻ tia OM.
Vì tam giác OAB cân tại O và OM là đường trung tuyến nên OM cũng là đường phân giác của ∠(AOB).
Vậy OM là tia phân giác của ∠(xOy).
Bài 89: Cho hình dưới trong đó giao điểm O của hai đường thẳng a và b nằm ngoài phạm vi tờ giấy. Chỉ vẽ hình trong phạm vi tờ giấu, hãy vẽ đường thẳng d đi qua A sao cho đường thẳng d cũng đi qua O nếu kéo dài đường thẳng d ra ngoài phạm vi tờ giấy.
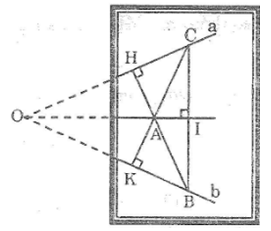
Lời giải:
- Kẻ AH ⊥ a kéo dài HA cắt b tại B
- Kẻ AH ⊥ b kéo dài KA cắt a tại C
- Kẻ AI ⊥ BC, đường thẳng AI đi qua O
Vì tam giác OBC có hai đường cao BH và CK cắt nhau tại A nên A là trực tâm của tam giác OBC.
Khi đó OA là đường cao thứ ba nên OA ⊥ BC.
Vì AI ⊥ BC nên đường thẳng OA và đường thẳng AI trùng nhau hay đường thẳng AI đi qua O.

