Bài 82, 83, 84 trang 52 SBT Toán 7 tập 2

Bài 82, 83, 84 trang 52 SBT Toán 7 tập 2

Bài 82: Cho tam giác ABC có AB < AC. Trên tia đối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA.

a. Hãy so sánh các góc AMB và ANC.

b. Hãy so sánh các độ dài AM và AN.

Lời giải:

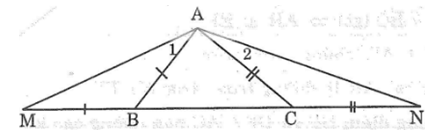
a. Trong ΔABC, ta có AB < AC

Suy ra: ∠(ABC) > ∠(ACB) (đối diện với cạnh lớn hơn là góc lớn hơn)    (1)

Ta có: AB = BM (gt) ⇒ ΔABM cân tại B

Suy ra: ∠(AMB) = ∠A₁ (tính chất tam giác cân)

Trong ΔABM, ta có ∠(ABC) là góc ngoài tại đỉnh B

Suy ra: ∠(ABC) = ∠(AMB) + ∠A₁

Suy ra: ∠(AMB) = 1/2 ∠(ABC)    (2)

Lại có: AC = CN (gt) ⇒ ΔACN cân tại C

Suy ra: ∠(ANC) = ∠A₂ (tính chất tam giác cân)

Trong ΔACN, ta có ∠(ACB) là góc ngoài tại đỉnh C

Suy ra: ∠(ACB) = ∠(ANC) + ∠A₂

Suy ra: ∠(ANC) = 1/2 ∠(ACB)    (3)

Từ (1), (2) và (3) suy ra: (AMB) > ∠(ANC) .

b. Trong ΔAMN, ta có: (AMB) > (ANC)

Suy ra: AN > AM (đối diện với góc lớn hơn là cạnh lớn hơn).

Bài 83: Cho tam giác ABC có AB < AC, đường cao AH. Chứng minh rằng: HB < HC, ∠(HAB) < ∠ (HAC) (xét hai trường hợp: B nhọn và B tù).

Lời giải:

Ta có: AB < AC (gt)

Suy ra: HB < HC (đường xiên lớn hơn thì hình chiếu lớn hơn)

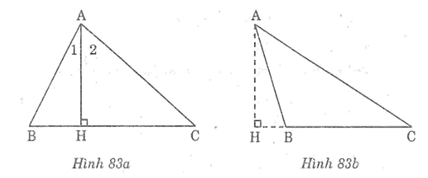
* Trường hợp Bnhọn (hình 83a)

Trong Δ ABC, ta có: AB < AC

Suy ra: ∠B > ∠C (đối diện với cạnh lớn hơn là góc lớn hơn)

Trong Δ AHB, ta có ∠(AHB) = 90°

Suy ra: ∠B + ∠(HAB) = 90° (tính chất tam giác vuông)    (1)

Trong Δ AHC, ta có ∠(AHC) = 90°

Suy ra: ∠C + ∠(HAC) = 90° (tính chất tam giác vuông)    (2)

Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)

Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC)

* Trường hợp Btù (hình 83b)

Vì điểm B nằm giữa H và C nên ∠(HAC) = ∠(HAB) + ∠(BAC)

Vậy ∠(HAB) < ∠(HAC).

Bài 84: Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài 1cm, 2cm, 3cm, 4cm, 5cm.

Lời giải:

Ta có: 1 = 3 - 2 = 4 - 3 = 5 - 4

Suy ra: trong 3 cạnh của tam giác không có cạnh nào có độ dài 1cm.

* Nếu cạnh nhỏ nhất là 2cm

Ta có: 4 - 3 < 2 < 4 + 3; 5 - 4 < 2 < 5 + 4

Suy ra: hai cạnh kia là 3cm và 4cm hoặc 4cm và 5cm

* Nếu cạnh nhỏ nhất là 3cm

Ta có: 5 - 4 < 3 < 5 + 4; 3 = 5 - 2; 3 > 4 - 2

Như vậy hai cạnh kia là 5cm và 4cm

* Không có trường hợp cạnh nhỏ nhất là 4cm

Vậy có thể vẽ được ba tam giác với độ dài các cạnh là:

    2cm; 3cm; 4cm

    2cm; 4cm; 5cm

    3cm; 4cm; 5cm